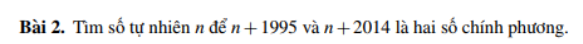Ta cần tìm số tự nhiên ( n ) sao cho ( n + 1995 ) và ( n + 2014 ) đều là số chính phương. Đặt:
n+1995=a2vaˋn+2014=b2
Trong đó ( a ) và ( b ) là các số nguyên. Ta có:
b2−a2=19
Sử dụng hằng đẳng thức hiệu hai bình phương:
(b−a)(b+a)=19
Vì 19 là số nguyên tố, nên chỉ có thể có các cặp số:
( b - a = 1 ) và ( b + a = 19 )( b - a = -1 ) và ( b + a = -19 )Xét trường hợp ( b - a = 1 ) và ( b + a = 19 ):
Giải hệ phương trình này:
b−a=1
b+a=19
Cộng hai phương trình:
2b=20⇒b=10
Thay ( b = 10 ) vào phương trình ( b - a = 1 ):
10−a=1⇒a=9
Vậy ( a = 9 ) và ( b = 10 ). Thay vào phương trình ( n + 1995 = 81 ):
n+1995=81⇒n=81−1995=−1914
Vì ( n ) phải là số tự nhiên, nên không có giá trị ( n ) thỏa mãn điều kiện này.
Kết luận: Không tồn tại số tự nhiên ( n ) nào để ( n + 1995 ) và ( n + 2014 ) đều là số chính phương.