cos (4x + 450) = - sinx
⇔ cos (4x + 450) = cos (x + 900)
⇔ \(\left[{}\begin{matrix}4x+45^0=x+90^0+k.360^0\\4x+45^0=-x-90^0+k.360^0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x=15^0+k.120^0\\x=-27^0+k.72^0\end{matrix}\right.\)
cos (4x + 450) = - sinx
⇔ cos (4x + 450) = cos (x + 900)
⇔ \(\left[{}\begin{matrix}4x+45^0=x+90^0+k.360^0\\4x+45^0=-x-90^0+k.360^0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x=15^0+k.120^0\\x=-27^0+k.72^0\end{matrix}\right.\)
Tìm GTLN - GTNN
1 . \(y=S\times\left(1-\frac{S^2-1}{2}\right)\)
2. \(y=\sin^4x+\cos^4x\)
3.\(y=\sin^6+\cos^6\)
4.\(y=\frac{\cos x+2\sin x+3}{2\cos x-\sin x+4}\)
Giải phương trình cos 4 x + 12 sin x . cos x - 5 = 0
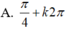
![]()
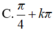
![]()
giải các phương trình sau :
1. sin( x+\(\pi\)/4)=2/3
2.cos2x-5sinx-3=0
3.cos3x=sin2x
4.cos3x=-\(\sqrt{ }\)3 với -\(\pi\)/2<x<0
5.4sin\(^4\)x + 12cos\(^2\)x=7
6.cot(x-1)=(cos2x)/(1+tanx) + sin\(^2\)x - 1/2sin2x
7.sin\(^2\)3x-cos\(^2\)4x=sin\(^2\)5x-cos\(^2\)6x
Giải phương trình:
\(\dfrac{1+cos2x\times cosx}{cos^2x}+2\left(sin^4x+cos^4x\right)=3\)
CMR: Biểu thức sau không phụ thuộc vào x: A=-sin⁴x +cos⁴x + 2sin²x B=sin⁴x + cos²x × sin²x + cos²x C= cos⁴x + cos²x × sin²x + cos²x
Tìm giới hạn B = lim x → 0 cos 2 x - cos 3 x x ( sin 3 x - sin 4 x )
A. +∞
B. -∞
C. 5/2
D. 0
Gải phương trình:
\(\sin\left(x\right)^3.2+\cos\left(2x\right)^3+\frac{1}{2}\sin\left(4x\right)=1\)
Giải các PT sau:
1. \(\dfrac{\left(2\cos2x-1\right)\left(\sin x-3\right)}{\sin x}=0\)
2.\(\dfrac{3\left(\sin x+\cos x\right)}{\sin x-\cos x}=2+2\cos x\)
3.\(\dfrac{3\left(\sin x+\tan x\right)}{\tan x-\sin x}-2\cos x=2\)
4. \(1+\sin x+\cos x+\sin2x+\cos2x=0\)
5. \(2\sin x\left(1+\cos2x\right)+\sin2x=1+2\cos x\)
Tìm tất cả các nghiệm của phương trình cos 3x + sin 2x – sin 4x = 0
![]()
![]()
![]()
![]()