s=r.r.3,14
c=d.3,14
r.r=c:3,14
r=c:3,14;2
c=r.2.3,14
d=r.2
d=c:3,14
r la ban kinh ,d la duong kinh ,c la chu vi, s la dien tich, . la nhan
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Diện tích S của hình tròn được tính bởi công thức S = πR2, trong đó R là bán kính của hình tròn.
Tính bán kính của hình tròn, làm tròn kết quả đến chữ số thập phân thứ hai, nếu biết diện tích của nó bằng 79,5 cm2.
Diện tích S của hình tròn được tính bởi công thức S = πR2, trong đó R là bán kính của hình tròn.
Nếu bán kính tăng gấp 3 lần thì diện tích tăng hay giảm bao nhiêu lần?
Diện tích hình tròn được tính theo công thức S=\pi R^2S=πR2 trong đó RR là bán kính của hình tròn. Một hình tròn có diện tích là 12,56 cm2. Bán kính hình tròn bằng....... cm.
(Lấy giá trị của \piπ là 3,14).
1. Hãy phát biểu bằng lời:a) Công thức tính diện tích xung quanh của hình trụ.b) Công thức tính thể tích của hình trụ.c) Công thức tính diện tích xung quanh của hình nón.d) Công thức tính thể tích của hình nón.e) Công thức tính diện tích của mặt cầu.f) Công thức tính thể tích của hình cầu.
Đọc tiếp
1. Hãy phát biểu bằng lời:
a) Công thức tính diện tích xung quanh của hình trụ.
b) Công thức tính thể tích của hình trụ.
c) Công thức tính diện tích xung quanh của hình nón.
d) Công thức tính thể tích của hình nón.
e) Công thức tính diện tích của mặt cầu.
f) Công thức tính thể tích của hình cầu.
Diện tích S của hình tròn được tính bởi công thức
S
π
R
2
, trong đó R là bán kính của hình tròn.a) Dùng máy tính bỏ túi, tính các giá trị của S rồi điền vào các ô trống trong bảng sau (π ≈ 3,14, làm tròn kết quả đến chữ số thập phân thứ hai).
R (cm)
0,57
1,37
2,15
4,09
S πR2
(Xem bài đọc thêm về máy tính bỏ túi dưới đây.)b) Nếu bán kính tăng gấp 3 lần...
Đọc tiếp
Diện tích S của hình tròn được tính bởi công thức S = π R 2 , trong đó R là bán kính của hình tròn.
a) Dùng máy tính bỏ túi, tính các giá trị của S rồi điền vào các ô trống trong bảng sau (π ≈ 3,14, làm tròn kết quả đến chữ số thập phân thứ hai).
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 |
(Xem bài đọc thêm về máy tính bỏ túi dưới đây.)
b) Nếu bán kính tăng gấp 3 lần thì diện tích tăng hay giảm bao nhiêu lần?
c) Tính bán kính của hình tròn, làm tròn kết quả đến chữ số thập phân thứ hai, nếu biết diện tích của nó bằng 79,5 cm2.
Viết công thức tính nửa góc ở đỉnh của một hình nón (góc α của tam giác vuông OAS – hình 99) sao cho diện tích mặt khai triển của mặt nón bằng một một phần tư diện tích của hình tròn (bán kính SA).
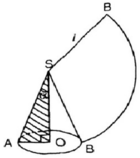
Hình 99
Viết công thức tính nửa góc ở đỉnh của một hình nón (góc α của tam giác vuông OAS – hình 99) sao cho diện tích mặt khai triển của mặt nón bằng một một phần tư diện tích của hình tròn (bán kính SA).
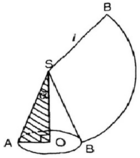
Hình 99
Diện tích S của hình tròn được tính bởi công thức S πR2, trong đó R là bán kính của hình tròn.Dùng máy tính bỏ túi, tính các giá trị của S rồi điền vào các ô trống trong bảng sau (π ≈ 3,14, làm tròn kết quả đến chữ số thập phân thứ hai).
R (cm)
0,57
1,37
2,15
4,09
S πR2
(Xem bài đọc thêm về máy tính bỏ túi dưới đây.)
Đọc tiếp
Diện tích S của hình tròn được tính bởi công thức S = πR2, trong đó R là bán kính của hình tròn.
Dùng máy tính bỏ túi, tính các giá trị của S rồi điền vào các ô trống trong bảng sau (π ≈ 3,14, làm tròn kết quả đến chữ số thập phân thứ hai).
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 |
(Xem bài đọc thêm về máy tính bỏ túi dưới đây.)
Cho tam giác đều và hình vuông cùng nội tiếp một hình tròn sao cho một cạnh của tam giác đều song song với một cạnh của hình vuông. Lập công thức tính diện tích phần giao nhau giữa tam giác đều và hình vuông khi biết bán kính r của đường tròn.