Các câu hỏi tương tự
các em giúp chị với 1 + 1 = 3 đúng không ạ,em học dốt lắm bị tụt lớp rùi,vào trang cá nhân em là biết ngu
có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
\(y=\dfrac{x-1}{\sqrt{mx^2-8x+2}}\) có đúng bốn đường tiệm cận (anh/chị giúp em câu này với.Em cảm ơn trước ạ )
Cho hàm số
y
x
4
-
m
x
2
+
m
(với m là tham số) có đồ thị là (C). Biết rằng khi
m
m
0
đồ thị (C) cắt trục hoành tại 4 điểm phân biệt có hoành độ
x
1
,
x
2
,
x
3
,
x...
Đọc tiếp
Cho hàm số y = x 4 - m x 2 + m (với m là tham số) có đồ thị là (C). Biết rằng khi m = m 0 đồ thị (C) cắt trục hoành tại 4 điểm phân biệt có hoành độ x 1 , x 2 , x 3 , x 4 thỏa mãn x 1 4 + x 2 4 + x 3 4 + x 4 4 = 30 . Hỏi mệnh đề nào sau đây là đúng?
A. 4 < m 0 ≤ 7
B. - 2 < m 0 < 4
C. m 0 > 7
D. m 0 ≤ - 2
tháng hai của một năm nào đó có 3 ngày thứ sáu đều là ngày lẻ. hỏi 24 của tháng đó là thứ mấy trong tuần
Cho hàm số y f(x) có đạo hàm liên tục trên R Đồ thị hàm số y f’(x) như hình bên dưới Đặt g(x) f(x) - x khẳng định nào sau đây là đúng? A. g(2) g( -1) g(1) B. g( -1) g(1) g(2) C. g(-1) g( 1) g( 2) D. g( 1) g( -1) g( 2)
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm liên tục trên R Đồ thị hàm số y= f’(x) như hình bên dưới
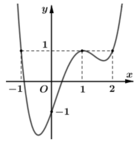
Đặt g(x) = f(x) - x khẳng định nào sau đây là đúng?
A. g(2) < g( -1) < g(1)
B. g( -1) < g(1) < g(2)
C. g(-1) > g( 1) > g( 2)
D. g( 1) < g( -1) < g( 2)
Cho hàm số
f
x
có đạo hàm liên tục trên R và có
f
1
-
1
,
f
-
1
-
1
3
Đặt
g
x
f
2
x
-
4
f
x
Cho biết đồ thị của
y
f...
Đọc tiếp
Cho hàm số f x có đạo hàm liên tục trên R và có f 1 - 1 , f - 1 = - 1 3 Đặt g x = f 2 x - 4 f x Cho biết đồ thị của y = f ' x có dạng như hình vẽ dưới đây
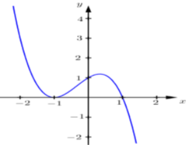
Mệnh đề nào sau đây đúng?
A. Hàm số g(x) có giá trị lớn nhất và không có giá trị nhỏ nhất trên R
B. Hàm số g(x) có giá trị nhỏ nhất và không có giá trị nhỏ nhất trên R
C. Hàm số g(x) có giá trị lớn nhất và giá trị nhỏ nhất trên R
D. Hàm số g(x) không có giá trị lớn nhất và giá trị nhỏ nhất trên R
Cho hàm số y f(x) có đạo hàm f’(x) liên tục trên [-2;1] Hình bên là đồ thị của hàm số y f’(x). Đặt
g
(
x
)
f
(
x
)
-
x
2
2
Khẳng định nào sau đây đúng? A. g(1) g(-2) g(0) B. g(0) g(1) g(-2) C. g(-2) g(1) g(0) D. g(0) g(-2) g(1)
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên [-2;1] Hình bên là đồ thị của hàm số y = f’(x). Đặt g ( x ) = f ( x ) - x 2 2
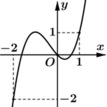
Khẳng định nào sau đây đúng?
A. g(1) < g(-2) < g(0)
B. g(0) < g(1) < g(-2)
C. g(-2) < g(1) < g(0)
D. g(0) < g(-2) < g(1)
Cho hàm số y f(x), biết tại các điểm A, B, C đồ thị hàm số y f(x) có tiếp tuyến được thể hiện trên hình vẽ. Mệnh để nào dưới đây là đúng?
Đọc tiếp
Cho hàm số y = f(x), biết tại các điểm A, B, C đồ thị hàm số y = f(x) có tiếp tuyến được thể hiện trên hình vẽ. Mệnh để nào dưới đây là đúng?
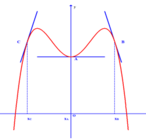
![]()
![]()
![]()
![]()
Cho hàm số y f(x) ax3+ bx2+cx+d có đạo hàm là hàm số y f’ (x) với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y f( x) tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y f( x) cắt trục tung tại điểm có tung độ là bao nhiêu? A. 2/3 B. 1 C. 3/2 D. 4/3
Đọc tiếp
Cho hàm số y= f(x) =ax3+ bx2+cx+d có đạo hàm là hàm số y= f’ (x) với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y= f( x) cắt trục tung tại điểm có tung độ là bao nhiêu?
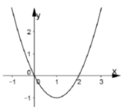
A. 2/3
B. 1
C. 3/2
D. 4/3





