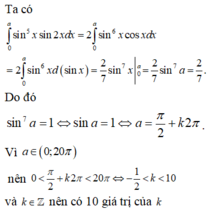Các câu hỏi tương tự
Cho f(x)
log
5
(
sin
x
)
,
x
∈
(
0
;
π
/
2
)
. Tính f(x)
Đọc tiếp
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
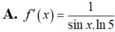
![]()
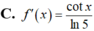
![]()
Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)2 + (
y
+
3
)2 + (z + 2)2 72. Mặt phẳng (P): x + by + cz + d 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là: A. b + c + d 2 B. b + c + d 4 C. b + c + d 3 D. b + c + d 1
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)2 + ( y + 3 )2 + (z + 2)2 = 72. Mặt phẳng (P): x + by + cz + d = 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là:
A. b + c + d = 2
B. b + c + d = 4
C. b + c + d = 3
D. b + c + d = 1
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
Cho A(4; 0; 0), B(0; 2; 0), C(0; 0; 1) và D(2; 2; 0). Có bao nhiêu tam giác vuông có ba đỉnh là ba trong số 5 điểm O, A, B, C, D.
Đọc tiếp
Cho A(4; 0; 0), B(0; 2; 0), C(0; 0; 1) và D(2; 2; 0). Có bao nhiêu tam giác vuông có ba đỉnh là ba trong số 5 điểm O, A, B, C, D.
![]()
![]()
![]()
![]()
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(
v
ớ
i
a
,
b
,
c
,
d
∈
ℝ
,
a...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y
sin
2
/
3
x
, y 0 và x
π
/2 bằng:A. 1; B. 2/7;C. 2
π
; D. 2
π
/3.
Đọc tiếp
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π /2 bằng:
A. 1; B. 2/7;
C. 2 π ; D. 2 π /3.
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
1.Tính các giá trị biểu thức sau:a)510000.log52-59999.log52-...-53.log52-52.log52?b)(x2+1).4100000-(x2+1).499999,5-...-(x2+1).43.5-(x2+1).43?c)(π+e).256500000-(π+e).256499999.875-...-(π+e).2561.125-256(π+e)?d)(frac{1}{pi}.1650000-frac{1}{pi}.1649999.75-...-frac{1}{pi}.162.25-frac{1}{pi}.162).(π.4150000-π.4149999.5-...-π.44.5-π.44)?e)(x-2).(sqrt{x+1})100000-(x-2).(sqrt{x+1})99999.5-...-(x-2).(sqrt{x+1})4.5-(x-2).(sqrt{x+1})4?f)(1/x)5.(1/2)-150000-(1/x)5.(1/2)-149999-...-(1/x)5.(1/2)-6-(1/x)5.(1/2...
Đọc tiếp
1.Tính các giá trị biểu thức sau:
a)510000.log52-59999.log52-...-53.log52-52.log52=?
b)(x2+1).4100000-(x2+1).499999,5-...-(x2+1).43.5-(x2+1).43=?
c)(π+e).256500000-(π+e).256499999.875-...-(π+e).2561.125-256(π+e)=?
d)(\(\frac{1}{\pi}\).1650000-\(\frac{1}{\pi}\).1649999.75-...-\(\frac{1}{\pi}\).162.25-\(\frac{1}{\pi}\).162).(π.4150000-π.4149999.5-...-π.44.5-π.44)=?
e)(x-2).(\(\sqrt{x+1}\))100000-(x-2).(\(\sqrt{x+1}\))99999.5-...-(x-2).(\(\sqrt{x+1}\))4.5-(x-2).(\(\sqrt{x+1}\))4=?
f)(1/x)5.(1/2)-150000-(1/x)5.(1/2)-149999-...-(1/x)5.(1/2)-6-(1/x)5.(1/2)-5=?
2.Giải ptrình bậc cao sau:
a)x.(x2+y)150000-x.(x2+y)149999-...-x.(x2+y)2-x3-xy-2=0
b)xy(2y+1)50000-xy(2y+1)49999-...-xy(2y+1)2-2xy2-3=0
c)x2(x+1)10000-x2(x+1)9999-...-x2(x+1)2-x2(x+1)-x2-1=0
d)x.(\(\sqrt{x+1}\))10000-x.(\(\sqrt{x+1}\))9998-...-x.(\(\sqrt{x+1}\))4-x-3=0
e)x50000-x49998-x49996-x49994-...-x8-x6-x4-x2-2=0
f)1+x+x2+...+x49998+x49999+x50000=0
g)(-2x)500000-(-2x)499999-...-(-2x)2+2(x-1)=0
h)(2x)100000-(x2)99999.5-...-(2x)1-(x2)0.5-2=0
i)cos(-x-1)100000+sin(-x-1)99999-cos(-x-1)99998+...-cos(-x-1)2+sin(-x-1)-1=0
k)(22^x)100000-(22^x)99999.99805-...-(22^x)0.001953125-2=0
l)(e3x/8+πx/3)250000-(e3x/8+πx/3)249999-...-(e3x/8+πx/3)2-e3x/8-πx/3-2=0
3.Tính giá trị tại vị trí gián đoạn sau:
a)250000-249999-...-24-23=?Biết gián đoạn tại vị trí thứ 4
b)710000.log72-79999.log72-...-72.log72-7log72=?Biết gián đoạn tại vị trí 3->5
c)22+23+...+24999+25000=?Biết gián đoạn tại vị trí thứ 350 và vị trí 600
4.Thực hiện các yêu cầu sau:
Cho pt M: x.(x+1)50000-x.(x+1)49999-...-x.(x+1)3-x.(x+1)2-n=0
a.Xác định x=?
b.Tính n=?
c.Số nào dưới đây là số nguyên tố:
A.n+1/n-1
B.n+2/n-2
C.n+3/n-3
D.n+4/n-4
d.Xác định phương trình đồng dạng bậc 20(¶20)?
5.Cho ptrình bậc 2 sau:x2-2x=0
a.Xác định hàm P=?
A.P=(x-1)2(x^2-2x) B.P=(x2-2x)/(x2-2x) C.P=2xx^2 D.(x2-2x)x^2-2x
b.Xác định hàm P(x)?Biết Q(x)=2x+1
A.P(x)=2x B.P(x)=2.(x+1) C.P(x)=2.(x+2) D.P(x)=2.(x+3)
c.Tính lim(P/Q(x))=?
A.0 B.1 C.2 D.3
d.Ptrình bậc cao:250000-249999-...-22-21 ~ vs hàm nào cuả pt bậc 2?
A.2P=2(x-1)x^2-2x B.2P=2.x2.2x C.2P=2.22x D.2P=2.42x
e.Đồ thị hàm bậc cao nằm trên:
A.Trục tung B.Trục hoành C.A,B đúng D.A,C sai
f.Khi nào P=P(x)?
A.Q(x)=0 B.P(x)=0 C.P=0 D.Q(x)=P
g.Hãy biến ptrình bậc 3 sau về ptrình bậc cao:x3-x=0?
A.(x3-x)50000-(x3-x)49999-...-(x3-x)2-x3-x=0
B.(x3-x)50000-(x3-x)49999-...-(x3-x)2-x3+x=0
C.(x3+x)50000-(x3+x)49999-...-(x3+x)2-x3-x=0
D.(x3+x)50000-(x3+x)49999-...-(x3+x)2-x3+x=0
h.Từ ptrình bậc 3 ở câu g so sánh P1=(x+e)x^3-x và P2=(x+e)3.(x^3-x)
A.P1>P2 B.P1=P2 C.P1<P2 D.P1~P2
i.Từ câu h,hãy tính giá trị biểu thức sin(P1-1)+cos(P2-1)+tan(P1P2-P1-P2+1)=?
A.-3 B.-1 C.1 D.3
6.Khai triển luỹ thừa bậc cao sau sang hàm bậc cao: 42949672961000000000?
7.Giải hệ ptrình:
Cho \(\alpha\)=\(\delta\)=25650000-25649999.875-...-2560.125-1
\(\beta\)=\(\mu\)=4100000-499999.5-...-4-40.5
\(\xi\)=\(\sigma\)=16500000-16499999.75-...-160.75-160.5
\(\hept{\begin{cases}\alpha\chi+\beta\gamma=\xi\\\sigma\chi+\mu\gamma=\delta\end{cases}}\)
8.Trả lời câu hỏi sau:
a.Công thức tìm cơ số tiêu chuẩn cuả hàm bậc cao là:
A.22^x B.44^x C.1616^x D.256256^x
b.Độ biến thiên theo cơ số tiêu chuẩn cuả hàm bậc cao là:
A.1/2x B.1/4x C.1/16x D.1/256x
c.Cho cơ số a=1,157920892.1077 ứng với độ biến thiên nào sau đây:
A.1/16 B.1/256 C.1/65536 D.1/16777216
d.Cho độ biến thiên ∆=1/250000 ứng vs cơ số tiêu chuẩn nào sau đây:
A.22^50000 B.44^25000 C.1616^12500 D.256256^6250
e.Giá trị cuả hằng số trực chuẩn là:
A.0 B.1 C.2 D.3
f.Miền trực chuẩn bất định ¢(a,∆)(a khác 0,1,2) được tính theo cthức nào sau đây:
A.¢(a,∆)=a.∆x B.¢(a,∆)=a.∆1/x C.¢(a,∆)=1/a.∆x D.¢(a,∆)=1/a.∆1/x
g.Miền trực chuẩn bất định ¢(a,∆)(a khác 0,1,2) luôn dần về:
A.0 B.1 C.2 D.3
h.Miền trực chuẩn cố định ¢(a,∆)(a=0;a=1;a=2) luôn dần về:
A.a B.∆ C.0 D.1
i.Một phương trình bậc cao có nghiệm khi và chỉ khi:
A.Có cùng cơ số ứng với độ biến thiên,có cùng hệ số,miền trực chuẩn luôn dần về một giá trị cố định không thay đổi,không có tính đồng dạng
B.Có cùng cơ số ứng với độ biến thiên,có cùng hệ số,miền trực chuẩn luôn dần về giá trị cố định không thay đổi,có tính đồng dạng
C.Có cùng cơ số ứng với độ biến thiên bất kì,các hệ số bất kì,miền trực chuẩn luôn dần về giá trị cố định không thay đổi,có tính đồng dạng
D.Có cùng cơ số ứng với độ biến thiên bất kì,các hệ số bất kì,miền trực chuẩn luôn dần về giá trị xác định không thay đổi,không có tính đồng dạng
k.Giá trị biên dưới cuả miền trực chuẩn ¢(65536;1/16) để giá trị đạt giá trị đạt hằng số trực chuẩn tuyệt đối:
A.3 B.33 C.83 D.163
(Chú ý tuyệt đối=0,tương đối~0)
l.Xét ptrình sau:5.(x+y)50000-6.(x+y)49999-3.(x+y)49998-...-2(x+y)2-4.(x+y)-2=0
A.Ptrình vô nghiệm B.Ptrình vô số nghiệm C.Phương trình có 1 nghiệm D.Ptrình 50000 nghiệm phân biệt
Giúp mik với!!!
Cho hàm số y f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) m có nghiệm thuộc khoảng
0
;
π
là
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) = m có nghiệm thuộc khoảng 0 ; π là

![]()
![]()
![]()
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]