Các câu hỏi tương tự
Chỉ cần đáp án ạ
Có bao nhiêu giá trị nguyên của a để giới hạn
lim(\(\sqrt{n^2+a^2n}-\sqrt{n^2+\left(a+2\right)n+1}\)=0
A. 0
B. 2
C. 1
D. 3
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4cos^3 x - cos 2x + (m-3)cos x - 1 = 0 có đúng 4 nghiệm khác nhau thuộc khoảng (-π/2; π/2)
Xem chi tiết
Có bao nhiêu giá trị nguyên của a để
l
i
m
(
n
2
-
4
n
+
7
+
a
-
n
)
0
? A. 3 B. 1 C. 2 D. 0
Đọc tiếp
Có bao nhiêu giá trị nguyên của a để l i m ( n 2 - 4 n + 7 + a - n ) = 0 ?
A. 3
B. 1
C. 2
D. 0
Có bao nhiêu giá trị nguyên của m để pt sin2 x - sinx - 3 -m = 0 có nghiệm duy nhất thuộc [-π/2;π/2]
Cho dãy số (
u
n
) xác định bởi
u
1
0
và
u
n
+
1
u
n
+
4
n
+
3
,
∀
n
⩾
2
. Biết :
l
i
m
u...
Đọc tiếp
Cho dãy số ( u n ) xác định bởi u 1 = 0 và u n + 1 = u n + 4 n + 3 , ∀ n ⩾ 2 . Biết :
l i m u n + u 4 n + u 4 2 n + . . . + u 4 2018 n u n + u 2 n + u 2 2 n + . . . + 2 2018 n = a 2019 + b c với a,b,c là các số nguyên dương và b<2019. Tính giá trị S=a+b-c
A.S= -1
B.S=0
C.S=2017
D.S=2018
AB là đoạn vuông góc chung của 2 đường thẳng
∆
,
∆
chéo nhau,
A
∈
∆
;
B
∈
∆
, AB a. M là điểm di động trên
∆
N là điểm di động trên
∆
. Đặt
A
M
m
;
A
N
n
(
m
≥...
Đọc tiếp
AB là đoạn vuông góc chung của 2 đường thẳng ∆ , ∆ ' chéo nhau, A ∈ ∆ ; B ∈ ∆ ' , AB= a. M là điểm di động trên ∆ N là điểm di động trên ∆ ' . Đặt A M = m ; A N = n ( m ≥ 0 ; n ⩾ 0 ) Giả sử ta luôn có m 2 + n 2 = b với b>0; b không đổi. Xác định m, n để độ dài đoạn MN đạt giá trị lớn nhất.
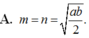
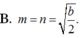
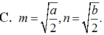
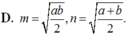
Câu 1: Tính giới hạn a, limdfrac{2-5^{n-2}}{3^n2.5^n} b,limdfrac{2-5^{n+2}}{3^n-2.5^n}Câu 2 :CMR :x^4+x^3-3x^2+x+10 có ít nhất một nghiệm âm lớn hơn -1Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Đọc tiếp
Câu 1: Tính giới hạn
a, lim\(\dfrac{2-5^{n-2}}{3^n=2.5^n}\) b,lim\(\dfrac{2-5^{n+2}}{3^n-2.5^n}\)
Câu 2 :CMR :\(x^4+x^3-3x^2+x+1=0\) có ít nhất một nghiệm âm lớn hơn -1
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Cho phương trình sinx(2-cos2x)-2(
2
cos
3
x
+m+1)
2
cos
3
x
+
m
+
2
3
2
cos
3
x
+
m
+
2
có bao nhiêu giá trị nguyên của tham số m để phương t...
Đọc tiếp
Cho phương trình sinx(2-cos2x)-2( 2 cos 3 x +m+1) 2 cos 3 x + m + 2 = 3 2 cos 3 x + m + 2 có bao nhiêu giá trị nguyên của tham số m để phương trình có đúng nghiệm thuộc [ 0 ; 2 π 3 ) ?
A. 1
B.2
C.3
D.4
Cho hàm số f(n) 1+3+6+10+...+
n
(
n
+
1
)
2
(
n
∈
N
*
)
. Biết lim
f
(
n
)
(
3
n
+
1
)...
Đọc tiếp
Cho hàm số f(n)= 1+3+6+10+...+ n ( n + 1 ) 2 ( n ∈ N * ) .
Biết lim f ( n ) ( 3 n + 1 ) ( 5 n 2 + 2 ) = a b ( a , b ∈ Z ) phân số này tối giản. Giá trị b - 5a là
A.50
B.45
C.85
D.60







