Các câu hỏi tương tự
Có bao nhiêu giá trị m nguyên để hàm số f(x)
2
x
2
+
m
x
+
2
3
2
xác định với mọi
x
∈
ℝ
? A. 5 B. 4 C. 7 D. 9
Đọc tiếp
Có bao nhiêu giá trị m nguyên để hàm số f(x) = 2 x 2 + m x + 2 3 2 xác định với mọi x ∈ ℝ ?
A. 5
B. 4
C. 7
D. 9
Có tất cả bao nhiêu giá trị nguyên của m để giá trị lớn nhất của hàm số
y
x
3
-
x
2
+
(
m
2
+
1
)
x
-
4
m...
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của m để giá trị lớn nhất của hàm số y = x 3 - x 2 + ( m 2 + 1 ) x - 4 m - 7 trên đoạn [ 0; 2]m không vượt quá 15 ?
A. 4
B . 6
C. 5
D. 8
Có bao nhiêu giá trị m nguyên để hàm số
f
(
x
)
2
x
2
+
m
x
+
2
3
2
xác định với mọi
x
∈
R
A. 5 B. 4. C. 7 D. 9
Đọc tiếp
Có bao nhiêu giá trị m nguyên để hàm số f ( x ) = 2 x 2 + m x + 2 3 2 xác định với mọi x ∈ R
A. 5
B. 4.
C. 7
D. 9
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
x
+
6
x
+
5
m
nghịch biến trên khoảng
10
;
+
∞
A. 5. B. 3. C. 4. D. Vô số.
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x + 6 x + 5 m nghịch biến trên khoảng 10 ; + ∞
A. 5.
B. 3.
C. 4.
D. Vô số.
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x + 6 x + 5 m nghịch biến trên khoảng 10 ; + ∞
A. 5
B. 3
C. 4
D. Vô số
Giá trị nhỏ nhất của hàm số \(y=\sqrt{4-x}+\sqrt{3}\) trên tập xác định của nó là
A: 2 + \(\sqrt{3}\)
B: 2\(\sqrt{3}\)
C: 0
D: \(\sqrt{3}\)
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) (x-6)
x
2
+
4
trên đoạn [0;3] có dạng a - b
c
với a là số nguyên và b, c là các số nguyên dương. Tính S a + b + c. A. 4 B. -2 C. -22 D. 5
Đọc tiếp
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = (x-6) x 2 + 4 trên đoạn [0;3] có dạng a - b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b + c.
A. 4
B. -2
C. -22
D. 5
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên. A. 1 B. 0 C. 2 D. 4
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số ![]() có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên.
có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên.
A. 1
B. 0
C. 2
D. 4
Cho hàm số f(x) liên tục trên [-1;3] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên [-1;3]. Tính M - m.
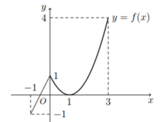
A. 3
B. 4
C. 5
D. 1





