Rút gọn biểu thức ta có:
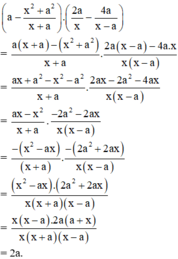
Với a là một số nguyên thì giá trị biểu thức bằng 2a là một số chẵn.
Rút gọn biểu thức ta có:
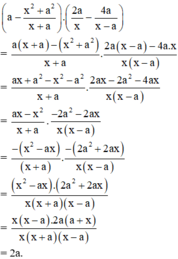
Với a là một số nguyên thì giá trị biểu thức bằng 2a là một số chẵn.
Chứng tỏ rằng với mọi x ≠ 0 và x ≠ ±a (a là một số nguyên), giá trị của biểu thức ( a-x^2+a^2/x+a) . ( 2a/x - 4a/x-a ) là một số chẵn
cho hai biểu thức a= x^2-x+5 và b=(x-1)(x+2)-x(x-2)-3x a, tính giá trị của biểu thức A khi x=2 b, chứng tỏ rằng B=-2 với mọi giá trị của biến x
Chứng tỏ với x ≠ 0 và x ≠ ± a (a là một số nguyên), giá trị của biểu thức: P = a − x 2 + a 2 x + a . 4 a x − 8 a x − a là một số chẵn.
cho biểu thức A= \(\dfrac{1}{x-2}+\dfrac{1}{x+2}+\dfrac{x^2+1}{x^2-4}\) (x ≠ 2, x ≠ -2)(biểu thức rút gọn là A=\(\dfrac{x-1}{x+2}\))
Chứng tỏ rằng với mọi x thỏa mãn: -2 < x < 2, x ≠ -1 phân thức luôn có giá trị âm
a, Tìm giá trị nguyên của x để biểu thức A = \(\frac{^{x^2+4}}{x-1}\)( với x khác 1) có giá trị là 1 số nguyên
b, Cho các số a,b,c khác 0 thỏa mãn: a+b+c = 0 và biểu thức:
P=\(\frac{ab}{a^2+b^2-c^2}\)+\(\frac{bc}{b^2+c^2-a^2}\)+\(\frac{ca}{c^2+a^2-b^2}\)
Chứng minh rằng: Giá trị của P khi được xác định luôn là một số hữu tỉ
Cho biểu thức :
A=(x2 + 2)2 _ (x - 2).(x + 2).(x2 + 4)
a. Rút gọn biểu thức A
b. Tính giá trị của A khi x = -2 , x=0 , x=2
c Chứng minh rằng A luôn có giá trị dương với mọi x
Cho hai biểu thức: A= \(\dfrac{1}{x-1}+\dfrac{-4}{x+1}+\dfrac{8x}{x^2-1}\) với x ≠ ±1
a) Chứng minh rằng A= \(\dfrac{5}{x-1}\)
b) Tính giá trị của A tại x thỏa mãn điều kiện |x-2|=3
c) Tìm giá trị nguyên của x để A có giá trị là một số nguyên.
cho biểu thức A=1/x-2+1/x+2+x^2+1/x^2-4 ( với x khác cộng trừ 2)
a) rút gọn biểu thức A
b) Chứng tỏ rằng với mọi x thỏa mãn -2<x<2, x khác -1 phân thức luôn có giá trị âm.
a) Tìm giá trị nhỏ nhất của biểu thức: A=x^2+3x-5
b) Chứng minh rằng A(x)=1/120x^5 -1/24 x^4+1/14x^3+1/24x^2-1/20x nhận giá trị nguyên với mọi giá trị nguyên của x