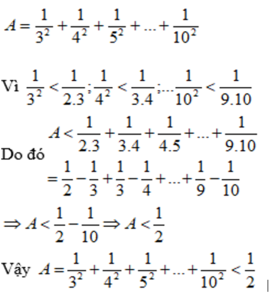Các câu hỏi tương tự
Cho A = 1/2+1/2^2+1/2^3+1/2^4+......+1/2^10
Chứng tỏ rằng A + 1/2^10 = 1
14 tháng 7 2021 lúc 18:39
Cho A = \(\dfrac{1}{2}\) + \(\dfrac{1}{2^{2}}\)+ \(\dfrac{1}{2^{3}}\)+ \(\dfrac{1}{2^{4}}\) + ...+ \(\dfrac{1}{2^{10}}\)
Chứng tỏ rằng A + \(\dfrac{1}{2^{10}}\)= 1
Chứng tỏ rằng :A=1/2^2+1/3^2+1/4^2+...+1/10^2<1
Xem chi tiết
1. Chứng minh rằng : 1/5 +1/14 +1/28 +1/44 +1/61+ 1/85 +1/91 < 1/2
2. Chứng tỏ rằng : 1/5+1/6+1/7+...+1/16+1/17 < 2
3. Tính: A= [878787/9595953+ (-8787/9595)] * 1234621/5678765
4. So sánh : 10^8+2/10^8-1 ; B= 10^8/10^8-3
Bài 7: Chứng tỏ rằng:1/2^2 + 1/3^2 + 1/4^2 + ...1/100^2 3/4Bài 8: So sánh A 20^10 + 1 / 20^10 - 1 và B 20^10 - 1 / 20^10 - 3.
Đọc tiếp
Bài 7: Chứng tỏ rằng:
1/2^2 + 1/3^2 + 1/4^2 + ...1/100^2 < 3/4
Bài 8: So sánh A= 20^10 + 1 / 20^10 - 1 và B= 20^10 - 1 / 20^10 - 3.
CHo A=1/3^2+1/4^2+1/5^2+...+1/50^2. Chứng tỏ rằng 1/4<A<4/9
Cho A = 1/2^2 + 1/3^2 + 1/4^2 + ........ + 1/100^2
Chứng tỏ rằng 3/5 < A < 3/4
11 tháng 4 2021 lúc 15:06
text{Bài 4. Chứng tỏ rằng:}a) dfrac{1}{2^2}+dfrac{1}{3^2}+dfrac{1}{4^2}+...+dfrac{1}{30^2} 1b) dfrac{1}{10}+dfrac{1}{11}+dfrac{1}{12}+...+dfrac{1}{99}+dfrac{1}{100}1c) dfrac{1}{5}+dfrac{1}{6}+dfrac{1}{7}+...+dfrac{1}{17} 2d) dfrac{1}{1.2}+dfrac{1}{2.3}+dfrac{1}{3.4}+...+dfrac{1}{29.30} 1
Đọc tiếp
\(\text{Bài 4. Chứng tỏ rằng:}\)
\(a\)) \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{30^2}< 1\)
\(b\)) \(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{99}+\dfrac{1}{100}>1\)
\(c\)) \(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 2\)
\(d\)) \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{29.30}< 1\)
Cho A = 1/2^2+1/3^2+1/4^2+...+1/100^2. Hãy chứng tỏ rằng 1/2<A <4/5
chứng tỏ rằng:(1/2 mũ 2+1/3 mũ 2 +1/3 mũ 2+1/4 mũ 2+1/5 mũ 2+1/6 mũ 2+1/7 mũ 2 +1/8 mũ 2+1/9 mũ 2+1/10 mũ 2)<1