Các câu hỏi tương tự
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
mạng mạng
Chứng minh rằng nếu trong tam giác ABC có hai cạnh AB và AC không bằng nhau thì đường trung tuyến xuất phát từ đỉnh A không vuông góc với BC.
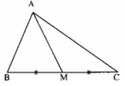
Chứng minh rằng nếu trong tam giác ABC có hai cạnh AB và AC không bằng nhau thì đường trung tuyến xuất phát từ đỉnh A không vuông góc với BC
chứng minh trong 1 tam giác,đường phân giác trong góc trong xuất phát từ mỗi đỉnh và hai đường phân giác ngoài xuất phát từ hai đỉnh kia đồng quy tại 1 điểm
Chứng minh rằng: Trong 1 tam giác vuông khi và chỉ khi 2 phân giác cắt nhau tạo 1 góc = 45 độ
Chứng minh rằng: Nếu 1 tam giác có đường cao và đường trung tuyến ứng với 1 cạnh (xuất phát từ 1 đỉnh) chia góc ở đỉnh đó thành 3 phần bằng nhau thì tam giác ấy vuông
Chứng minh rằng một tam giác có hai đường đường cao(xuất phát từ các đỉng của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
bài 1: chứng minh 1 tam có 2 đường trung tuyến bằng nhau thì tam giác đó cân
bài 2: chứng minh trong tam giác cân 2 đường cao ứng với 2 cạnh bên và ngược lại có 2 đường cao bằng nhau là tam giác cân
bài 3:chứng minh 2 đường phân giác xuất phát từ 2 đỉnh ở đấy của tam giác cân thì bằng nhau và ngược lại 1 tam giác có 2 đg phân giác bằng nhau thì là tam giác ân
Gi sử có một đường thẳng đi qua đỉnh A của tam giác ABC và chia tam giác ABC thành hai tam giác có các góc tương ứng bằng nhau. Chứng minh rằng tam giác ABC là tam giác vuông hoặc có góc B bàng góc C













