Question

Chứng minh rằng mọi đường thẳng đi qua trung điểm của đường trung bình của hình thang và cắt hai dây hình thang sẽ chia hình thang đó thành hai hình thang có diện tích bằng nhau.

Answer 1

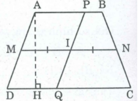
Giả sử hình thang ABCD có AB // CD, đường trung bình là MN. Gọi I là trung điểm của MN, đường thẳng bất kỳ đi qua I cắt AB tại P và CD tại Q.

Ta có hai hình thang APQD và BPQC có cùng đường cao.

MI là đường trung bình của hình thang APQD.

Suy ra: MI = 1/2 (AP + QD)

IN là đường trung bình của hình thang BPQC.

Suy ra: IN = 1/2 (BP + QC)

S A P Q D  = 1/2 (AP + QD).AH = MI.AH (1)

S B P Q C  = 1/2 (BP + QC).AH = IN.AH (2).

IM = IN (gt) (3)

Từ (1), (2) và (3) suy ra: S A P Q D = S B P Q C , các giá trị này không phụ thuộc vào vị trí của P và Q.