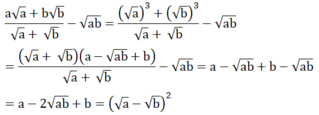Các câu hỏi tương tự
Chứng minh các đẳng thức sau:
a
)
1
−
a
a
1
−
a
+
a
1
−
a
1
−...
Đọc tiếp
Chứng minh các đẳng thức sau:
a ) 1 − a a 1 − a + a 1 − a 1 − a 2 = 1 v ớ i a ≥ 0 v à a ≠ 1 b ) a + b b 2 a 2 b 4 a 2 + 2 a b + b 2 = | a | v ó i a + b > 0 v à b ≠ 0
Chứng minh các đẳng thức sau:
a
)
2
3
−
6
8
−
2
−
216
3
⋅
1
6
−
1
,
5
b
)...
Đọc tiếp
Chứng minh các đẳng thức sau:
a ) 2 3 − 6 8 − 2 − 216 3 ⋅ 1 6 = − 1 , 5 b ) 14 − 7 1 − 2 + 15 − 5 1 − 3 : 1 7 − 5 = − 2 c ) a b + b a a b : 1 a − b = a − b v ó i a , b d ư ơ n g v à a ≠ b . d ) 1 + a + a a + 1 ⋅ 1 − a − a a − 1 = 1 − a v ó i a ≥ 0 v à a ≠ 1
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: ![]()
b) Cho a, b, c > 0. Chứng minh rằng: ![]()
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab
Chứng minh đẳng thức:
a
a
+
b
b
a
+
b
-
a
b
a
-
b
2
v...
Đọc tiếp
Chứng minh đẳng thức: a a + b b a + b - a b = a - b 2 v ớ i a > 0 , b > 0
Chứng minh các đẳng thức sau:
a
+
b
b
2
a
2
b
4
a
2
+
2
a
b
+...
Đọc tiếp
Chứng minh các đẳng thức sau: a + b b 2 a 2 b 4 a 2 + 2 a b + b 2 = a v ớ i a + b > 0 v à b ≠ 0
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: \(\frac{a+b}{2}\ge\sqrt{ab}\)
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy:
b) Cho a, b, c > 0. Chứng minh rằng:
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
Cho các số thực a,b,c thỏa mãn a+b+c=0. Chứng minh đẳng thức:
(a²+b²+c²)²=2(a⁴+b⁴+c⁴).
a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8