Đặt y = 3(cos x – 1) + 2sinx + 6
Hàm số xác định, liên tục và có đạo hàm tại mọi x ∈ R
Ta có: y( π ) = 0 và y' = -3sin x + 2cos x + 6 > 0, x ∈ R.
Hàm số đồng biến trên R và có một nghiệm x = π
Vậy phương trình đã cho có một nghiệm duy nhất.
Chứng minh các phương trình sau có nghiệm duy nhất
3(cosx − 1) + 2sinx + 6x = 0
Phương trình nào sau đây có nghiệm duy nhất trên R?
A. x 2 - 7x + 12 = 0 B. x 3 + 5x + 6 = 0
C. x 4 - 3 x 2 + 1 = 0 D. 2sinx. cos 2 x - 2sinx - cos 2 x + 1 = 0
Phương trình nào sau đây có nghiệm duy nhất trên R?
A. (x - 5)( x 2 - x - 12) = 0 B. - x 3 + x 2 - 3x + 2 = 0
C. sin 2 x - 5sinx + 4 = 0 D. sinx - cosx + 1 = 0
Phương trình nào sau đây có nghiệm duy nhất trên R?
A. (x - 5)( x 2 - x - 12) = 0 B. - x 3 + x 2 - 3x + 2 = 0
C. sin 2 x - 5sinx + 4 = 0 D. sinx - cosx + 1 = 0
Trong các phương trình sau cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2).
B. (1).
C. (3).
D. (1) và (2).
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2)
B. (1)
C. (3)
D. (1) và (2)
Tìm tất cả các giá trị của tham số a để phương trình sau có nghiệm duy nhất a log 3 x 3 + 4 log 3 x 8 + a + 1 = 0
A. a=1.
B. a<-1.
C. Không tồn tại a.
D. a<1.
Số nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2 sin x + 1 = 0 trên khoảng - π 2 ; 3 π 2 bằng:
A. 2
B. 4
C. 3
D. 1
Cho hàm số f(x) có đạo hàm liên tục trên ℝ và thỏa mãn f(x) > 0, ∀ x ∈ ℝ . Biết f(0) = 1 và f ' ( x ) = ( 6 x - 3 x 2 ) f ( x ) . Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có nghiệm duy nhất.
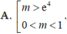
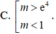
