Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π /2);
x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π /2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
Chứng minh các bất đẳng thức sau:
a) tanx > sinx, 0 < x < π/2
b)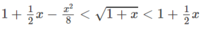 
với 0 < x < + ∞
Chứng minh các bất đẳng thức sau: tan x > x 0 < x < π 2
Chứng minh các bất đẳng thức sau: tan x > x + x 3 3 0 < x < π 2
Chứng minh các bất đẳng thức sau:
1 + 1 2 x - x 2 8 < 1 + x < 1 + 1 2 x
với 0 < x < + ∞
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π} và {y = x + sinx, y = x với π ≤ x ≤ 2π}
b) {y = sinx, y = 0 với 0 ≤ x ≤ π} và {y = cosx, y = 0 với 0 ≤ x ≤ π};
c) {y = √x, y = x 2 }
và {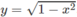 
, y = 1 − x}
Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox: y = 2x/ π ; y = sinx; x ∈ [0; π /2]
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = -π/4 và x = π/4 bằng:
A. π; B. -π;
C. ln2; D. 0
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = - π /4 và x = π /4 bằng:
A. π ; B. - π ;
C. ln2; D. 0
