Với mọi a ∈ R , ta có:
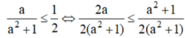
⇔ 2a ≤ a2 + 1 (do 2(a2 + 1) > 0)
⇔ a2 - 2a + 1 ≥ 0 ⇔ (a - 1)2 ≥ 0 là bất đẳng thức đúng.
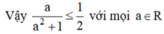
Với mọi a ∈ R , ta có:
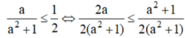
⇔ 2a ≤ a2 + 1 (do 2(a2 + 1) > 0)
⇔ a2 - 2a + 1 ≥ 0 ⇔ (a - 1)2 ≥ 0 là bất đẳng thức đúng.
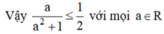
Cho ∆ABC vuông tại A (AB < AC) có M và E lần lượt là trung điểm của BC và AC, vẽ MD vuông góc với AB tại D.
a) Ch ứ ng minh: ME // AB và t ứ giác ADME là hình ch ữ nh ậ t.
b) G ọ i K là đi ể m đ ố i x ứ ng v ớ i M qua E. T ứ giác AMCK là hình gì? Ch ứ ng minh.
c) G ọ i O là giao đi ể m c ủ a AM và DE, H là hình chi ế u c ủ a M trên AK. Ch ứ ng minh: HD HE
Cho hình bình hành ABCD có
0
60
ˆ
=
A
, AD = 2AB. G i M là trung đi m c a AD, N là trung đi m c a BC.
ọ ể ủ ể ủ
-
3
-
a.
Ch ng minh t giác MNCD là hình thoi
ứ ứ
b.
T C k đ ng th ng vuông góc v i MN t i E, c t AB t i F. Ch bg minh E là trung đi m c a CF
ừ ẻ ườ ẳ ớ ạ ắ ạ ứ ể ủ
c.
Ch ng minh
ứ
∆
MCF đ u
ề
d.
Ch ng minh ba đi m F, N, D th ng hàng
Cho tam giác ABC có AB = 5cm.Trên cạnh AB, Ac lần luotj lấy 2 điểm M,N sao cho AM = 3cm,AN=7,5cm, NC = 5cm.
a) Chứng minh MN // BC
b) Gọi I,K lần lượt là trung điểm MN,BC.Chứng minh A,I,K thẳng hàng
Giúp minh vs .Mai kiểm tra r
Tam giác ABC vuông cân tại A ,M là 1 điểm trên AC ,I là trung điểm của BM ,N là trung điểm của AC .Đường thẳng đi qua A và vuông góc với IN căt đường thẳng đi qua C và vuông góc với AC tại E .chứng minh IN=1/2 AEtam giác ABC vuông cân tại A ,M là 1 điểm trên AC ,I là trung điểm của BM ,N là trung điểm của AC .Đường thẳng đi qua A và vuông góc với IN căt đường thẳng đi qua C và vuông góc với AC tại E .chứng minh IN=1/2 AE
cho tam giác ABC có trung tuyến AM ,điểm I thuộc đoạn thẳng AM ,BI cắt AC ở I
a) nếu AD = 1/2 DC chứng minh I là trung điểm AM
b) nếu I là trung điểm AM chứng minh AD = 1/2 DC , ID=1/4 BD
c) nếu AD = 1/2 DC khi đó trên cạnh AD lấy điểm E sao cho AB =3AE chứng minh BD, CE,AM đồng quy
Cho tam giác ABC . M,N lần lượt là trung điểm của AC và AB . Gọi I là giao điểm của BM và CN .
a, Chứng minh rằng MN song song với BC ; MN = 1/2 BC
b, Gọi K là diểm đối xứng với I qua M . Tứ giác AKCI là hình gì ? Vì sao ?
c, Gọi P đối xứng với A qua I . Chứng minh rằng A,P,D thẳng hàng .
Cho tam giác ABC cân tại A. M là trung điểm của AB . Từ M kẻ ME song song với BC,cắt AC tại E
a) Chứng minh tứ giác BMEC là hình thang cân
b) từ M kẻ MF song song với AC cắt BC tại F. Chứng minh tứ giác MECF là hình bình hành.
c) gọi I là trung điểm của MF. Chứng minh B,I,E thẳng hàng.
d) MC cắt EF tại K kẻ KH vuông góc với ME(H thuộc ME). Chứng minh FK^2=KH^2+1/4 IK^2.
Chứng minh rằng a/ a mũ 2 +1 nhỏ hơn hoặc bằng 1 /2 với mọi a thuộc R
Cho 3 điểm A, B, C theo thứ tự nằm trên đường thẳng d biết AB < BC. Trong cùng một nửa mặt phẳng bờ là đường thẳng d vẽ 2 tam giác đều ADB và BEC. Gọi M, N, P, Q, I theo thứ tự là trung điểm của các đoạn thẳng BD, AE, BE, CD và DE.
a) Chứng minh 3 điểm I, M, N thẳng hàng ; I, Q, P thẳng hàng
b) Chứng minh tứ giác MNPQ là hình thanh cân
c) Chứng minh NQ=1/2 DE
Cho hình vuông ABCD có cạnh là a. M là một điểm nằm trên đường chéo BD; E,F là hình chiếu của M trên AB và AD; BF và CE cắt nhau tại I.
a/ Chứng minh: CE=BF, CM=EF
b/ Chứng minh: Khi M thay đổi trên BD thì I luôn cách 1 điểm cố định một khoảng bằng a/2. Hãy tìm điểm cố định đó
c/ Chứng minh: Các đường thẳng: BF, CM, DE đồng quy