a) Ta có:
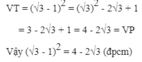
b) Theo câu a) ta có:
![]()
= |√3 - 1| - √3 = √3 - 1 - √3
= -1 = VP (vì √3 - 1 > 0) (đpcm)
a) Ta có:
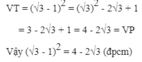
b) Theo câu a) ta có:
![]()
= |√3 - 1| - √3 = √3 - 1 - √3
= -1 = VP (vì √3 - 1 > 0) (đpcm)
Chứng minh rằng:
a) \(\frac{2^3-1}{2^3+1}.\frac{3^3-1}{3^3+1}...\frac{n^3-1}{n^3+1}>\frac{2}{3}\)
b) \(\frac{1}{1^4+4}+\frac{1}{3^4+4}+...+\frac{2n+1}{\left(2n+1\right)^4+4}< \frac{1}{4}\)
1)chứng minh rằng nếu a+b+c=1 thì a^4 +c^4 +b^4 =abc
2) với a,b,c dương chứng minh rằng 2căna +2cănb+2cănc +a^2+b^2+c^2 >= 3(a+b+c)
Cho a,b,c >0 thỏa mãn abc=1. Chứng minh
\(\frac{1}{\sqrt{a^4-a^3+ab+2}}+\frac{1}{\sqrt{b^4-b^3+bc+2}}+\frac{1}{\sqrt{c^4-c^3+ca+2}}\le\sqrt{3}\)
1, cho a,b,c>0. chứng minh \(a^4+b^4+c^4\ge abc\left(a+b+c\right)\)
2, chứng minh: với mọi a,b \(\ne0\)\(\frac{a^2}{b^2}+\frac{b^2}{a^2}\ge\frac{a}{b}+\frac{b}{a}\)
3,cho các số thực \(\in\)đoạn 0 đến 1. chứng minh:\(a^4+a^3+c^2-ab-bc-ca\le1\)
4,cho a,b,c là các số thực dương tùy ý. chứng minh: \(\frac{a^3+b^3}{ab}+\frac{b^3+c^3}{bc}+\frac{c^3+a^3}{ca}\ge2\left(a+b+c\right)\)
5,cho a,b,c>0. chứng minh\(\frac{a}{bc}+\frac{b}{ac}+\frac{c}{ab}\ge2\left(\frac{1}{a}+\frac{1}{b}-\frac{1}{c}\right)\)
ai làm đk bài nào thì làm hộ e vs ạ
Cho 3 số thực dương a,b,c nhỏ hơn 4
Chứng minh:
\(\frac{1}{4-a}+\frac{1}{4-b}+\frac{1}{4-c}\ge\frac{3}{4}+\frac{a^2+b^2+c^2}{16}\)
Bài 1: Chứng Minh Rằng : \(\sqrt[3]{\sqrt[3]{2}-1}\)= \(\sqrt[3]{\frac{1}{9}}-\sqrt[3]{\frac{2}{9}}+\sqrt[3]{\frac{4}{9}}\)
Bài 2: Rút gọn biểu thức:
A= \(\frac{a^3-3a+\left(a^2-1\right)\sqrt{a^2-4}-2}{a^3-3a+\left(a^2-1\right)\sqrt{a^2-4}+2}\)( với a>2)
B= \(\sqrt{\frac{1}{a^2+b^2}+\frac{1}{\left(a+b\right)^2}+\sqrt{\frac{1}{a^4}+\frac{1}{b^4}+\frac{1}{\left(a^2+b^2\right)^2}}}\)(ab # 0)
1.Chứng minh \(\sqrt{x^2+xy+y^2}+\sqrt{x^2+xz+z^2}\ge\sqrt{y^2+yz+z^2}\)
2. Cho a,b,c>0. Chứng minh \(\left(\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}\right)\left(\frac{1}{\sqrt[3]{a}}+\frac{1}{\sqrt[3]{b}}+\frac{1}{\sqrt[3]{c}}\right)-\frac{a+b+c}{\sqrt[3]{abc}}\le6\)
3. Cho a,b>0 , n là số nguyên dương. Chứng minh \(\frac{1}{\sqrt[n]{a}}+\frac{1}{\sqrt[n]{b}}\ge2\sqrt[n]{\frac{2}{a+b}}\)
4. Cho a,b,c >0. Chứng minh \(\frac{1}{a^2+bc}+\frac{1}{b^2+ca}+\frac{1}{c^2+ba}\le\frac{a+b+c}{2abc}\)
Cho các số dương a,b,c cs abc=1 Chứng minh rằng
\(\dfrac{a^3}{\left(b+2\right)\left(c+3\right)}+\dfrac{b^3}{\left(c+2\right)\left(a+3\right)}+\dfrac{c^3}{\left(a+2\right)\left(b+3\right)}\ge\dfrac{1}{4}\)
a)Cho a>b>0 chứng minh rằng \(\frac{1}{a+b}\le\frac{1}{2\sqrt{ab}}\)
b) Chứng minh \(\frac{\sqrt{2}-\sqrt{1}}{3}+\frac{\sqrt{3}-\sqrt{2}}{5}+\frac{\sqrt{4}-\sqrt{3}}{7}+...+\frac{\sqrt{2011}-\sqrt{2010}}{4021}< \frac{1}{2}\)
cho 3 số a, b, c>0, và a+b+c=3. chứng minh rằng:
\(\frac{a^4}{\left(a+2\right)\left(b+2\right)}+\frac{b^4}{\left(b+2\right)\left(c+2\right)}+\frac{c^4}{\left(c+2\right)\left(a+2\right)}\ge\frac{1}{3}\)
giải giup minh nhe