Các câu hỏi tương tự
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
1. cos 2a + cos 2b - 2 cos(a+b) cos( a-b)
2. cos2a + sin2b 1
3. cos a2 + sin b2 1
4. cos2 a + sin2 a 1
5. cos 2a cos2 a - 2 sin 2a
6. sin 2a - 2 sin a. cos a.
7. sin 2a cos2 a - sin2 a
8. sin 2a - sin 2b 2 sin ( a+b) cos ( a - b)
9. sin 2a - sin 2b 2 cos( a+b) sin ( a - b)
10. cos a2 + sin a2 1
Câu số mấy đúng?
Đọc tiếp
1. cos 2a + cos 2b = - 2 cos(a+b) cos( a-b)
2. cos2a + sin2b = 1
3. cos a2 + sin b2= 1
4. cos2 a + sin2 a = 1
5. cos 2a = cos2 a - 2 sin 2a
6. sin 2a = - 2 sin a. cos a.
7. sin 2a = cos2 a - sin2 a
8. sin 2a - sin 2b= 2 sin ( a+b) cos ( a - b)
9. sin 2a - sin 2b= 2 cos( a+b) sin ( a - b)
10. cos a2 + sin a2 = 1
Câu số mấy đúng?
Cho hai số thực a và b thỏa mãn a b và
∫
a
b
x
sin
x
d
x
π
đồng thời a cos a 0 và
b
cos
b
-
π
.Tính tích phân
∫
a
b
cos
x
d
x
. A.
I
-
π
.
B.
I...
Đọc tiếp
Cho hai số thực a và b thỏa mãn a < b và ∫ a b x sin x d x = π đồng thời a cos a = 0 và b cos b = - π .Tính tích phân ∫ a b cos x d x .
A. I = - π .
B. I = π .
C. I = 145 12 .
D. I = 0.
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:A.
π
(
a
2
+
b
2
+
c
2
) B. 2
π
(
a...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:
A. π ( a 2 + b 2 + c 2 ) B. 2 π ( a 2 + b 2 + c 2 )
C. 4 π ( a 2 + b 2 + c 2 ) D. π /2.( a 2 + b 2 + c 2 )
Cho hình lập phương ABCD.ABCD. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó:
V
H
V
ABCD
.
A
B
C
D...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó: V H V ABCD . A ' B ' C ' D '
A. 1/3 B. π /6
C. π /8 D. π /12
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:A. 2
π
a
3
B. 2
π
a
3
/3C. 4
π
a
3
D.
π
a
3
Đọc tiếp
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:
A. 2 π a 3 B. 2 π a 3 /3
C. 4 π a 3 D. π a 3
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y
sin
2
/
3
x
, y 0 và x
π
/2 bằng:A. 1; B. 2/7;C. 2
π
; D. 2
π
/3.
Đọc tiếp
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π /2 bằng:
A. 1; B. 2/7;
C. 2 π ; D. 2 π /3.
Cho f(x)
log
5
(
sin
x
)
,
x
∈
(
0
;
π
/
2
)
. Tính f(x)
Đọc tiếp
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
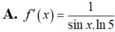
![]()
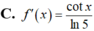
![]()
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình bên. Phương trình f( 2 sin x) m có đúng ba nghiệm phân biệt thuộc đoạn
-
π
;
π
khi và chỉ khi A.
m
∈
-
3
;
1
B.
m
∈
-...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f( 2 sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
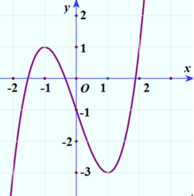
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = -π/4 và x = π/4 bằng:
A. π; B. -π;
C. ln2; D. 0