Question

Cho x,y là các số thực dương thỏa mãn điều kiện  5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y x - 2

Tính giá trị nhỏ nhất của biểu thức T =x + y.

A. T m i n = 2 + 3 2

B. T m i n = 3 + 2 3

C. T m i n = 1 + 5

D. T m i n = 5 + 3 2

Answer 1

Từ giả thiết ta suy ra

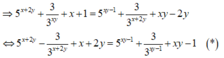
Xét hàm số  f ( t ) = 5 t - 1 3 t + t   với  t   ∈ ℝ ,   f ' ( t ) = 5 t . ln 5 + 3 - t . ln 3 + 1 > 0 ;   ∀ t ∈ ℝ

Suy ra y= f( t) là hàm số đồng biến trên R mà từ ( * ) suy ra

f (x+ 2y) =f( xy-1)  hay x+ 2y= xy-1

với x>0 suy ra y>1.

Khi đó

 

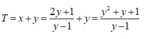
Xét hàm số

  f ( y ) = y 2 + y + 1 y - 1   t r ê n   1 ; + ∞ f ' y = y 2 - 2 y - 2 y - 1 2 = 0 ⇔ y = ± 1 + 3 f 1 + 3 = 3 + 2 3 ;   lim y → 1 f ( y ) = lim y → + ∞ f ( y ) = + ∞

Do đó, giá trị nhỏ nhất của hàm số là  3 + 2 3 .

Vậy kết quả là  3 + 2 3

Chọn B.