Các câu hỏi tương tự
B1)Tứ giác ABCD có ADBC, các tia DA và CB cắt nhau tại O. Gọi I, K theo thứ tự là trung điểm của AB, CD. Đường thẳng IK cắt các đường thẳng AD, BC theo thứ tự ở E,F. CMR; OEF là tam giác cânB2) Hình thang ABCD (AB//CD) có ABa, CDb, BC c, AD d. Các tia phân giác của các góc A và D cắt nhau ở E. Các tia phân giác của các góc B và C cắt nhau ở F. Gọi M, N theo thứ tự là trung điểm của AD, BC.a)CMR: 4 điểm M, E, F, N thẳng hàngb) Tính các độ dài MN, MF, FN theo a,b,c,dc) CMR: a+b c+d thì E trùng vớ...
Đọc tiếp
B1)Tứ giác ABCD có AD=BC, các tia DA và CB cắt nhau tại O. Gọi I, K theo thứ tự là trung điểm của AB, CD. Đường thẳng IK cắt các đường thẳng AD, BC theo thứ tự ở E,F. CMR; OEF là tam giác cân
B2) Hình thang ABCD (AB//CD) có AB=a, CD=b, BC= c, AD= d. Các tia phân giác của các góc A và D cắt nhau ở E. Các tia phân giác của các góc B và C cắt nhau ở F. Gọi M, N theo thứ tự là trung điểm của AD, BC.
a)CMR: 4 điểm M, E, F, N thẳng hàng
b) Tính các độ dài MN, MF, FN theo a,b,c,d
c) CMR: a+b= c+d thì E trùng với F
B3) Cho hình thang ABCD (AB//CD) có AB= AD+BC. CMR: các tia phân giác của góc C,D cắt nhau tại một điểm trên cạnh AB.
Hình thang ABCD(AB//CD) có AB=a, BC=b, CD=c, AD=d. các tia phân giác góc A và D cắt nhau tại E. các tia phân giác góc B và góc C cắt nhau tại F. gọi M, N là trung điểm của AD, BC. a. Chứng minh tam giác AED vuông. b. Chứng minh rằng nếu E trùng với F thì a+b=c+d.
Cho tứ giác ABCD có góc A = góc C = 90 độ, các tia DA, CB cắt nhau tại E, các tia AB,CD cắt nhau tại F
a ) Chứng minh góc E = góc F
b ) Tia phân giác của góc E cắt AB,CD tại G và H
Tia phân giác của góc F cắt BC,AD theo thứ tự tại I và K. Chứng minh GHKI là hình thoi.
Cho hình thang ABCD (AB//CD). Gọi M, N tương ứng là trung điểm
của AD, BC. Các phân giác góc A, D cắt nhau tại E, các phân giác góc B, C cắt nhau tại
F. Chứng minh rằng
a) Các góc AED, BFC vuông;
b) M, N, E, F thẳng hàng;
c) Nếu AB + CD = AD + BC thì E trùng F.
Cho tứ giác ABCD, biết 2 đường thẳng AB và CD cắt nhau tại E, hai đường thẳng BC và AD cắt nhau ở F. Các phân giác của ^E và^F cắt nhau ở I. Chứng minh:
a, ˆEIF=ˆABC+ˆADC/2
b, Nếu ˆBAD=130 độ và ^BCD =50 độ thì IE vuông góc với IF.
Cho tứ giác ABCD có góc A = góc C = 90 độ , các tia DA và CB cắt nhau tại E , các tia AB và DC cắt nhau tại F
a, C/m E = F
b, Tia phân giác của góc E cắt AB ,CD theo thứ tự ở G và H . Tia phân giác của góc F cắt BC ,AD theo thứ tự ở I và K . Chứng minh GKHI là hình thoi
Cho tứ giác ABCD có góc A = góc C = 90 độ , các tia DA và CB cắt nhau tại E , các tia AB và DC cắt nhau tại F
a, C/m E = F
b, Tia phân giác của góc E cắt AB ,CD theo thứ tự ở G và H . Tia phân giác của góc F cắt BC ,AD theo thứ tự ở I và K . Chứng minh GKHI là hình thoi
Bài 1: Tứ giác ABCD, góc A góc C90 độ. Da cắt CB tại E, AB cắt CD tại F. Chứng minh rằng:a) Góc E góc Fb) Tia phân giác của góc E cắt AB tại G, cắt CD tại H. Tia phân giác của góc F cắt BC tại I,cắt AD tại K.CMR: GKHI là hình thoiBài 2: Tam giác ABC đều. M thuộc BC, ME vuông góc với AB (E thuộc AB). ME vuông góc với AC (F thuộc AC). I thuộc AM: IAIM. D thuộc BC: DBDC. Chứng minh rằng:a) Góc DIE, góc DIF?b) DEIF là hình thoiBài 3: Tam giác ABC, D thuộc AB, E thuộc AC: BDCE. M thuộc DE: MDME. N th...
Đọc tiếp
Bài 1: Tứ giác ABCD, góc A =góc C=90 độ. Da cắt CB tại E, AB cắt CD tại F. Chứng minh rằng:
a) Góc E= góc F
b) Tia phân giác của góc E cắt AB tại G, cắt CD tại H. Tia phân giác của góc F cắt BC tại I,cắt AD tại K.
CMR: GKHI là hình thoi
Bài 2: Tam giác ABC đều. M thuộc BC, ME vuông góc với AB (E thuộc AB). ME vuông góc với AC (F thuộc AC). I thuộc AM: IA=IM. D thuộc BC: DB=DC. Chứng minh rằng:
a) Góc DIE, góc DIF=?
b) DEIF là hình thoi
Bài 3: Tam giác ABC, D thuộc AB, E thuộc AC: BD=CE. M thuộc DE: MD=ME. N thuộc BC: NB=NC. I thuộc BE: IB=IE. K thuộc CD: KC=KD. Chứng minh rằng:
a) MINK là hình?
b) IK cắt AB tại G, IK cắt AC tại H
CMR: Tam giác AGH cân
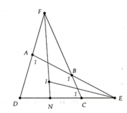
Cho tứ giác ABCD. Biết 2 đường thẳng AD cắt BC tại E, AB cắt CD tại F. Các tia phân giác góc E và F cắt nhau tại I. Tính góc EIF thep góc A và C