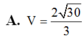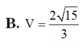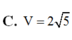Các câu hỏi tương tự
Cho tứ diện O.ABC có cạnh OA, OB, OC đôi một vuông góc với nhau. Biết OA2cm, OB3cm, OC6cm. Tính thể tích của khối tứ diện O.ABC A.
6
c
m
3
B.
36
c
m
3
C.
12
c
m
3
D.
18
c
m
3
Đọc tiếp
Cho tứ diện O.ABC có cạnh OA, OB, OC đôi một vuông góc với nhau. Biết OA=2cm, OB=3cm, OC=6cm. Tính thể tích của khối tứ diện O.ABC
A. 6 c m 3
B. 36 c m 3
C. 12 c m 3
D. 18 c m 3
Xét tứ diện O.ABC có OA, OB, OC đôi một vuông góc. Gọi
α
,
β
,
γ
lần lượt là góc giữa các đường thẳng OA, OB, OC với mặt phẳng (ABC). Khi đó, tính giá trị nhỏ nhất của biểu thức sau M (3+
c
o
t
2
α
)(3+
c
o
t
2
β
)(3+
c
o
t...
Đọc tiếp
Xét tứ diện O.ABC có OA, OB, OC đôi một vuông góc. Gọi α , β , γ lần lượt là góc giữa các đường thẳng OA, OB, OC với mặt phẳng (ABC). Khi đó, tính giá trị nhỏ nhất của biểu thức sau M= (3+ c o t 2 α )(3+ c o t 2 β )(3+ c o t 2 γ )
A. Số khác
B. 48 3
C. 48
D. 125
Cho khối chóp O.ABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Biết OA = 1, OB = 2 và thể tích khối chóp O.ABC bằng 3. Độ dài cạnh OC bằng:
A. 3 2
B. 9 2
C. 9
D. 3
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết OAa, OB2a và đường thẳng AC tạo với mặt phẳng (OBC) một góc
60
0
. Thể tích khối tứ diện OABC bằng
Đọc tiếp
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết OA=a, OB=2a và đường thẳng AC tạo với mặt phẳng (OBC) một góc 60 0 . Thể tích khối tứ diện OABC bằng
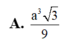
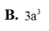
![]()
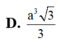
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA
a
2
2
, OBOCa. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Tính thể tích khối tứ diện OABH. A.
a
3
2
6
B.
a
3...
Đọc tiếp
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA = a 2 2 , OB=OC=a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Tính thể tích khối tứ diện OABH.
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Mệnh đề nào sau đây đúng? A. H là trọng tâm tam giác ABC . B. H là trung điểm của BC. C. H là trực tâm của tam giác ABC. D. H là trung điểm của AC.
Đọc tiếp
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Mệnh đề nào sau đây đúng?
A. H là trọng tâm tam giác ABC .
B. H là trung điểm của BC.
C. H là trực tâm của tam giác ABC.
D. H là trung điểm của AC.
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng A.
90
0
B.
30
0
C.
60
0
D.
45
0
Đọc tiếp
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
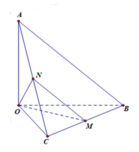
A. 90 0
B. 30 0
C. 60 0
D. 45 0
Cho tứ diện O.ABC cos OA, OB, OC đôi một vuông góc và OB = OC = a 6 , OA = a. Khi đó góc giữa hai mặt phẳng bằng
A. 300.
B. 900.
C. 450.
D. 600.
Có một khối gỗ dạng hình chóp O.ABC có OA, OB, OC đôi một vuông góc với nhau, OA 3cm, OB 6cm, OC 12cm. Trên mặt (ABC) người ta đánh dấu một điểm M sau đó người ta cắt gọt khối gỗ để thu được một hình hộp chữ nhật có OM là một đường chéo đồng thời hình hộp có 3 mặt nằm trên 3 mặt của tứ diện (xem hình vẽ). Thể tích lớn nhất của khối gỗ hình hộp chữ nhật bằng: A. 8
c
m
3
B. 24
c
m
3
C. 1...
Đọc tiếp
Có một khối gỗ dạng hình chóp O.ABC có OA, OB, OC đôi một vuông góc với nhau, OA = 3cm, OB = 6cm, OC = 12cm. Trên mặt (ABC) người ta đánh dấu một điểm M sau đó người ta cắt gọt khối gỗ để thu được một hình hộp chữ nhật có OM là một đường chéo đồng thời hình hộp có 3 mặt nằm trên 3 mặt của tứ diện (xem hình vẽ).
Thể tích lớn nhất của khối gỗ hình hộp chữ nhật bằng:

A. 8 c m 3
B. 24 c m 3
C. 12 c m 3
D. 36 c m 3