Đáp án B.
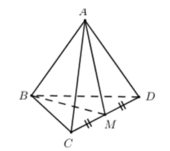
- Phương pháp: Tứ diện đều có các cặp cạnh đối vuông góc.
- Cách giải:
+ Gọi M là trung điểm của CD ta có:
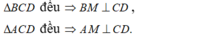
+ Ta có:
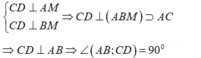
Đáp án B.

- Phương pháp: Tứ diện đều có các cặp cạnh đối vuông góc.
- Cách giải:
+ Gọi M là trung điểm của CD ta có:
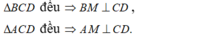
+ Ta có:
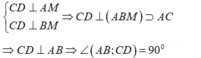
Tứ diện đều ABCD số đo góc giữa hai đường thẳng AB và CD bằng
![]()
![]()
![]()
![]()
Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD là
A. 45⁰.
B. 90⁰.
C. 60⁰.
D. 30⁰.
Cho tứ diện ABCD có AB=AC=AD và B A C ^ = B A D ^ = 60 ° . Xác định góc giữa hai đường thẳng AB và CD
![]()
![]()
![]()
![]()
Cho tứ diện đều ABCD cạnh a. Tính khoảng cách giữa hai đường thẳng AB và CD
A. a 2
B. a 2
C. a
D. a 2 2
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau, biết AB=AC=AD=1. Số đo góc giữa hai đường thẳng AB và CD bằng
A. 45 ⁰ .
B. 60 ° .
C. 30 ⁰ .
D. 90 ⁰ .
Cho tứ diện ABCD có AB = CD =a. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30 0
A. MN = a 2
B. MN = a 3 2
C. MN = a 3 3
D. MN = a 4
Cho tứ diện ABCD có AB = CD = a, I J = a 3 2 (I, J lần lượt là trung điểm của BC và AD). Số đo góc giữa hai đường thẳng AB và CD là:
Cho tứ diện đều ABCD cạnh a. Tính cosin góc giữa hai đường thẳng AB và CI với I là trung điểm của AD
A. 3 2
B. 3 6
C. 3 4
D. 1 2