Đáp án A
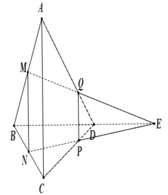
Gọi ![]() thì Q là giao điểm của (MNP) và AD.
thì Q là giao điểm của (MNP) và AD.
Áp dụng định lí Menelaus trong ∆ B C D ta có:
![]()
![]()
Áp dụng định lí Menelaus trong ∆ ABD ta có:
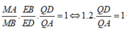
![]()
Đáp án A

Gọi ![]() thì Q là giao điểm của (MNP) và AD.
thì Q là giao điểm của (MNP) và AD.
Áp dụng định lí Menelaus trong ∆ B C D ta có:
![]()
![]()
Áp dụng định lí Menelaus trong ∆ ABD ta có:
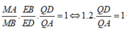
![]()
Cho tứ diện ABCD đều cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB, BC. Điểm P trên cạnh CD sao cho Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích của khối đa diện BMNPQD bằng
A. 11 2 216
B. 2 27
C. 5 2 108
D. 7 2 216
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Giao tuyến của hai mặt phẳng (MNP) và (ACD) là:
A. MP
B. NQ
C. MQ
D. AP
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Tỉ số QD/QC bằng:
A. 1/2
B. 3/4
C. 2/3
D. 3 2
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Đường thẳng MP không chéo với đường thẳng nào sau đây?
A. AB
B. CD
C. NP
D. BC
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Trên cạnh CD lấy
điểm P sao cho PD=2PC .
a) Tìm giao điểm của đường thẳng BD và mặt phẳng (MNP).
b) Tìm giao tuyến của mặt phẳng (MNP) và (ABD).
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Mặt phẳng α qua MN cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?
A. I; A; C
B. I; B; D
C. I; A: B
D. I; C; D
Cho tứ diện ABCD. Qua điểm M nằm trên AC ta dựng một mặt phẳng (α) song song với AB và CD. Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P và Q.
a) Tứ giác MNPQ là hình gì?
b) Gọi O là giao điểm hai đường chéo của tứ giác MNPQ. Tìm tập hợp các điểm O khi M di động trên đoạn AC.
câu 1 :Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và trên cạnh BC lấy điểm P sao cho BP = 2PC
a) Tìm giao tuyến của (MNP) với (ABD)
b) Tìm giao điểm của AD với (MNP). Từ đó xác định thiết diện của (MNP) với tứ diện
câu 2: Cho hình chóp tứgiác S.ABCD có AB và CD không song song. Gọi M là trung điểm của SD
a) Tìm giao tuyến của hai mp (SAC) và (SBD)
b) Tìm giao điểm của BM với (SAC)
c) Tìm giao điểm của (ABM) với SC
Câu 1 :Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và trên cạnh BC lấy điểm P sao cho BP = 2PC a) Tìm giao tuyến của (MNP) với (ABD) b) Tìm giao điểm của AD với (MNP). Từ đó xác định thiết diện của (MNP) với tứ diện