Đáp án B
Ta dễ có:
M N → = M A → + A D → + D N → M N → = M B → + B C → + C N →
![]()
Mà M và N lần lượt là trung điểm của AB và CD nên
![]()
Do đó 2 M N → = A D → + B C →
![]()
Đáp án B
Ta dễ có:
M N → = M A → + A D → + D N → M N → = M B → + B C → + C N →
![]()
Mà M và N lần lượt là trung điểm của AB và CD nên
![]()
Do đó 2 M N → = A D → + B C →
![]()
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ M N → = k ( A D → + B C → )
A. k = 3
B. k = 1 2
C. k = 2
D. k = 7 5
Gọi M, N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm đoạn MầM NON và P là 1 điểm bất kỳ trong không gian. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ I A → + ( 2 k - 1 ) I B → + k I C → + I D → = 0 → ?
A. k = 2
B. k = 4
C. k = 1
D. k = 0
Cho tứ diện đều ABCD cạnh a. Gọi K là trung điểm của AB, M, N lần lượt là hình chiều của K lên AD và AC. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp K.CDMN?
![]()
![]()
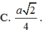
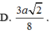
Trong không gian, cho hình thang cân ABCD có AB//CD, AB = a, CD = 2a, AD = a. Gọi M, N lần lượt là trung điểm của AB. CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thành ABCD quanh trục MN. Tính diện tích toàn phần S t p của khối K.
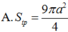
![]()
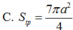
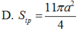
Cho hình chóp S. ABCD có đáy ABCD là hình thoi và có thể tích bằng 2. Gọi M, N lần lượt là các điểm trên cạnh SB và SD sao cho S M S B = S N S D = k . Tìm giá trị của k để thể tích khối chóp S.AMN bằng 1 8
A.k = 1 8
B.k = 2 2
C.k = 2 4
D.k = 1 4
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên BD lấy điểm K sao cho BK= 2KD. Gọi E là giao điểm của JK và CD; F là giao điểm của IE và AD. Tìm giao điểm của AD và (IJK).
A. Điểm I
B. Điểm E
C. Điểm F
D. Điểm K
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a với SA = a 2 , SB = a 3 2 , B A D ^ = 60 ∘ và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là trung điểm của AB, BC. Thể tích tứ diện K.SDC có giá trị là:

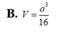
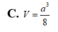
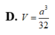
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
A. {0}
B. R
C. {-3}
D. (-3; +∞).
Cho hàm số y=x3-3x2+4 có đồ thị (C) . Gọi d là đường thẳng qua I(1; 2) với hệ số góc k . Có bao nhiêu giá trị nguyên của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
A. 4
B. 1
C. 6
D. vô số