Các câu hỏi tương tự
Cho tứ diện ABCD, G là trọng tâm của tam giác ABD, M là điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?
A. MG // (ACD)
B. MG // (ABC)
C. MG // AB
D. MG cắt AC
Cho tứ diện ABCD, G là trọng tâm tam giác ABD, N là trung điểm của AD, M là trung điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?
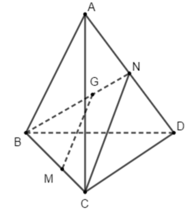
A. MG // CN
B. MG và CN cắt nhau
C. MG // AB
D. MG và CN chéo nhau.
Cho tứ diện ABCD với G là trọng tâm của tam giác ABD, M là điểm trên cạnh BC sao cho . Khi đó mệnh đề nào sau đây là đúng?
A. MG cắt CD.
B. MG//CD.
C. MG//(ACD)
D. MG cắt BD.
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. M là điểm trên cạnh BC sao cho MB=2MC. Khi đó đường thẳng MG song song với mặt phẳng nào dưới đây?
A. (ACD)
B. (BCD)
C. (ABD)
D. (ABC)
Cho tứ diện ABCD, G là trọng tâm
△
A
B
D
và M là điểm trên cạnh BC sao cho BM2MC Đường thẳng MG song song với mặt phẳng nào sau đây: A. (ABC) B. (ABD) C. (BCD) D. (ACD)
Đọc tiếp
Cho tứ diện ABCD, G là trọng tâm △ A B D và M là điểm trên cạnh BC sao cho BM=2MC Đường thẳng MG song song với mặt phẳng nào sau đây:
A. (ABC)
B. (ABD)
C. (BCD)
D. (ACD)
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. M thuộc đoạn thẳng BC sao cho BM = 2MC. Giao tuyến của mặt phẳng (BGM) và (ACD)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA 3a. Chọn hệ trục tọa độ Oxyz sao cho A trùng với O, điểm B thuộc tia Ox, điểm D thuộc tia Oy và điểm S thuộc tia Oz. Gọi G là trọng tâm của tam giác SBD. Mệnh đề nào dưới đây là đúng?
A
.
G
(
a
3
;
a
3
;
a
)
B
.
...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3a. Chọn hệ trục tọa độ Oxyz sao cho A trùng với O, điểm B thuộc tia Ox, điểm D thuộc tia Oy và điểm S thuộc tia Oz. Gọi G là trọng tâm của tam giác SBD. Mệnh đề nào dưới đây là đúng?
A . G ( a 3 ; a 3 ; a )
B . G ( a ; a ; 3 a )
C . G ( a 2 ; a 2 ; 3 a 2 )
D . G ( a 3 ; a ; a 3 )
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng:
A. GE//CD
B. GE và CD chéo nhau
C. GE cắt AD
D. GE cắt CD
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’.a) Chứng minh rằng AM song song với A’M’.b) Tìm giao điểm của mặt phẳng (A’B’C’) với đường thẳng A’M.c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’).d) Tìm giao điểm G của đường thẳng d với mp(AMA’). Chứng minh G là trọng tâm của tam giác AB’C’.
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’.
a) Chứng minh rằng AM song song với A’M’.
b) Tìm giao điểm của mặt phẳng (A’B’C’) với đường thẳng A’M.
c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’).
d) Tìm giao điểm G của đường thẳng d với mp(AMA’). Chứng minh G là trọng tâm của tam giác AB’C’.