Các câu hỏi tương tự
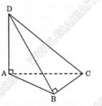
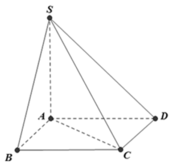
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (DBC) và
D
B
C
^
90
°
. Khi quay các cạnh của tứ diện xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
Đọc tiếp
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (DBC) và D B C ^ = 90 ° . Khi quay các cạnh của tứ diện xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có AD ⊥ (ABC) và BD ⊥ BC. Khi quay tất cả các cạnh của tứ diện đó quanh cạnh AB có những hình nón nào được tạo thành ? Hãy kể tên các hình nón đó.
Trong không gian cho tam giác OIM vuông tại I, góc
I
O
M
^
45
°
và cạnh
I
M
a
. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh
S
x
q
của hình nón tròn xoay đó theo a
Đọc tiếp
Trong không gian cho tam giác OIM vuông tại I, góc I O M ^ = 45 ° và cạnh I M = a . Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh S x q của hình nón tròn xoay đó theo a
![]()
![]()
![]()
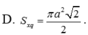
Trong không gian cho tam giác OIM vuông tại I, góc
I
O
M
^
45
o
và cạnh IM a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh Sxq của hình nón tròn xoay đó theo a
Đọc tiếp
Trong không gian cho tam giác OIM vuông tại I, góc I O M ^ = 45 o và cạnh IM = a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh Sxq của hình nón tròn xoay đó theo a
![]()
![]()
![]()
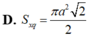
Cho tứ diện ABCD có AD ⊥ (ABC) và BD ⊥ BC. Khi quay tứ diện đó xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
A. Một B. Hai
C. Ba D. Bốn
Trong không gian cho tam giác OIM vuông tại I,
I
O
M
⏜
45
0
và cạnh IMa. Khi quay tam giác IOM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Khi đó diện tích xung quanh của hình nón tròn xoay đó bằng:
Đọc tiếp
Trong không gian cho tam giác OIM vuông tại I, I O M ⏜ = 45 0 và cạnh IM=a. Khi quay tam giác IOM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Khi đó diện tích xung quanh của hình nón tròn xoay đó bằng:
![]()
![]()
![]()
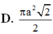
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy SC a
6
. Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là: A.
4
πa
3
3
B.
πa
3
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy SC = a 6 . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:
A. 4 πa 3 3
B. πa 3 2 6
C. πa 3 3 3
D. πa 3 6 3
Cho tam giác ABC vuông cân tại B, cạnh AB 2. Quay đường gấp khúc ACB quanh cạnh AB ta được hình nón. Tính diện tích xung quang của hình nón đó A.
8
π
2
.
B.
4
π
2
.
C.
4
π
3
.
D.
2
π
2
.
Đọc tiếp
Cho tam giác ABC vuông cân tại B, cạnh AB = 2. Quay đường gấp khúc ACB quanh cạnh AB ta được hình nón. Tính diện tích xung quang của hình nón đó
A. 8 π 2 .
B. 4 π 2 .
C. 4 π 3 .
D. 2 π 2 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy
S
C
a
6
. Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là: A.
4
πa
3
3
B.
a
3
π...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy S C = a 6 . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:
A. 4 πa 3 3
B. a 3 π 2 6
C. πa 3 3 3
D. πa 3 3 6