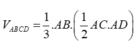Các câu hỏi tương tự
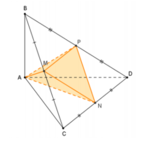
Cho tứ diện đều ABCD có cạnh bằng a, trên các cạnh AB, AC, AD lần lượt lấy các điểm M, N, P sao cho AB 2 AM, AN 2NC, AD 2 AP. Thể tích của khối tứ diện AMNP là: A.
a
3
2
72
B.
a
3
3
48
C. ...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a, trên các cạnh AB, AC, AD lần lượt lấy các điểm M, N, P sao cho AB = 2 AM, AN= 2NC, AD = 2 AP. Thể tích của khối tứ diện AMNP là:
A. a 3 2 72
B. a 3 3 48
C. a 3 2 48
D. a 3 2 12
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB a; AC a
2
; AD a
3
,(a0) Thể tích V của khối tứ diện ABCD là: A.
V
a
3
6
3
B. ...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB = a; AC =a 2 ; AD = a 3 ,(a>0) Thể tích V của khối tứ diện ABCD là:
A. V = a 3 6 3
B. V = a 3 6 6
C. V = a 3 6 2
D. V = a 3 6 9
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB 3a, AC 4a, AD5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a. A.
V
10
a
3
27
B.
V...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB =3a, AC = 4a, AD=5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.
A. V = 10 a 3 27
B. V = 80 a 3 27
C. V = 20 a 3 27
D. V = 40 a 3 27
Cho tứ diện ABCD có các cạnh BA, BC, BC đôi một vuông góc với nhau, BA 3a, BC BD 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM A. V 8
a
3
B. V
2
a
3
3
C. V
3
a
3
2
D. V...
Đọc tiếp
Cho tứ diện ABCD có các cạnh BA, BC, BC đôi một vuông góc với nhau, BA = 3a, BC = BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM
A. V = 8 a 3
B. V = 2 a 3 3
C. V = 3 a 3 2
D. V = a 3
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, ABa, ACb, ADc Tính thể tích V của khối tứ diện ABCD theo a, b, c
Đọc tiếp
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, AB=a, AC=b, AD=c Tính thể tích V của khối tứ diện ABCD theo a, b, c
![]()
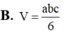
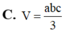
![]()
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh MN ⊥ AB và MN ⊥ CD. Mặt phẳng (CDM) có vuông góc với mặt phẳng (ABN) không? Vì sao?
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A
B
→
+
A
C
→
+
A
D
→
bằng: A.
4
A
G...
Đọc tiếp
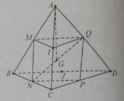
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A B → + A C → + A D → bằng:
A. 4 A G →
B. 2 A G →
C. A G →
D. 1 / 2 A G →
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho . Tính thể tích V của khối tứ diện PMNC
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho 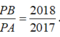 . Tính thể tích V của khối tứ diện PMNC
. Tính thể tích V của khối tứ diện PMNC
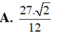

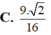

cho hình tứ diện ABCD có AB,AC,AD đôi một vuông góc và AB=AC=AD=5cm gọi M là trung điểm BC a) chứng minh BC vuông góc ADM b) tính khoảng cách từ điểm A đén BCD C) tính góc giữa đường thẳng DM và mặt phẳng ABC