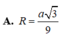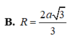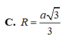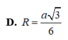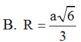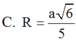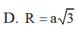Các câu hỏi tương tự
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là các tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, C và tiêp xúc với đường thẳng AD tại A. Bán kính R của mặt cầu (S) bằng
Đọc tiếp
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là các tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, C và tiêp xúc với đường thẳng AD tại A. Bán kính R của mặt cầu (S) bằng
![]()
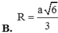
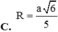
![]()
Cho tam giác vuông cân ABC có cạnh huyền AB = 2a. Trên đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC), lấy một điểm S khác A, ta được tứ diện SABC. Tính bán kính của mặt cầu ngoại tiếp tứ diện SABC trong trường hợp mặt phẳng (SBC) tạo với mặt phẳng (ABC) một góc bằng 300.
Cho tam giác ABC đều cạnh a , đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC). Gọi S là điểm thay đổi trên đường thẳng d , H là trực tâm tam giác SBC. Biết rằng khi điểm S thay đổi trên đường thẳng d thì điểm H nằm trên đường tròn (C). Trong số các mặt cầu chứa đường tròn (C) , bán kính mặt cầu nhỏ nhất là
Đọc tiếp
Cho tam giác ABC đều cạnh a , đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC). Gọi S là điểm thay đổi trên đường thẳng d , H là trực tâm tam giác SBC. Biết rằng khi điểm S thay đổi trên đường thẳng d thì điểm H nằm trên đường tròn (C). Trong số các mặt cầu chứa đường tròn (C) , bán kính mặt cầu nhỏ nhất là
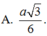
![]()
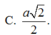
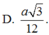
Trong mặt phẳng (P) cho tam giác OAB cân tại O, OAOB2a,
A
O
B
⏜
120
0
. Trên đường thẳng vuông góc với măt phẳng (P)tại O lấy hai điểm C, D, nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
Đọc tiếp
Trong mặt phẳng (P) cho tam giác OAB cân tại O, OA=OB=2a, A O B ⏜ = 120 0 . Trên đường thẳng vuông góc với măt phẳng (P)tại O lấy hai điểm C, D, nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
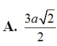
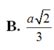
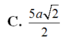
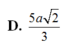
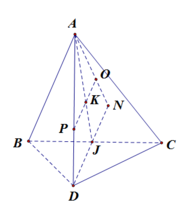
Cho hình tứ diện ABCD có hai tam giác ΔBCD, ΔACD là hai tam giác đều cạnh a và nằm trên hai mặt phẳng vuông góc với nhau. Bán kính mặt cầu ngoại tiếp hình tứ diện là: A.
a
7
2
B.
a
6
C.
a
5
6
D....
Đọc tiếp
Cho hình tứ diện ABCD có hai tam giác ΔBCD, ΔACD là hai tam giác đều cạnh a và nằm trên hai mặt phẳng vuông góc với nhau. Bán kính mặt cầu ngoại tiếp hình tứ diện là:
A. a 7 2
B. a 6
C. a 5 6
D. a 15 6
Hình chóp A.BCD có đáy ABC là tam giác vuông tại a, SA vuông góc với mặt phẳng (ABC), SA a, AB b, AC c. Tính bán kính R của mặt cầu đi qua các điểm A, B, C và S ? A.
R
2
(
a
+
b
+
c
)...
Đọc tiếp
Hình chóp A'.BC'D có đáy ABC là tam giác vuông tại a, SA vuông góc với mặt phẳng (ABC), SA = a, AB = b, AC = c. Tính bán kính R của mặt cầu đi qua các điểm A, B, C và S ?
A. R = 2 ( a + b + c ) 3
B. R = 2 a 2 + b 2 + c 2
C. R = 1 2 a 2 + b 2 + c 2
D. R = a 2 + b 2 + c 2
Cho mặt cầu (S) bán kính R5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
πcm
. Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
32
3
c
m
3
B.
60...
Đọc tiếp
Cho mặt cầu (S) bán kính R=5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 πcm . Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3
B. 60 3 c m 3
C. 20 3 c m 3
D. 96 3 c m 3
Cho hình chóp S.ABCD có tam giác ABC cân tại A, cạnh bên là a. Biết rằng khoảng cách từ đỉnh S tới mặt đáy (ABC) bằng hai lần đường cao kẻ từ đỉnh A của tam giác ABC đồng thời các vuông tại B và C. Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện S.ABC
Đọc tiếp
Cho hình chóp S.ABCD có tam giác ABC cân tại A, cạnh bên là a. Biết rằng khoảng cách từ đỉnh S tới mặt đáy (ABC) bằng hai lần đường cao kẻ từ đỉnh A của tam giác ABC đồng thời các vuông tại B và C. Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện S.ABC

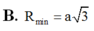
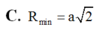

Cho lăng trụ tam giác ABC.ABC có đáy là tam giác đều cạnh bằng a, góc tạo bởi cạnh bên và mặt phẳng đáy bằng
30
∘
. Biết hình chiếu vuông góc của A trên (ABC) trùng với trung điểm cạnh BC. Tính theo a bán kính mặt cầu ngoại tiếp tứ diện A.ABC
Đọc tiếp
Cho lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh bằng a, góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30 ∘ . Biết hình chiếu vuông góc của A' trên (ABC) trùng với trung điểm cạnh BC. Tính theo a bán kính mặt cầu ngoại tiếp tứ diện A'.ABC