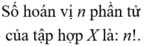Các câu hỏi tương tự
Cho tập hợp X = {1;2;3;4;…;n^3}. Chứng minh rằng, với mọi số tự nhiên n ≥ 2 luôn tồn tại tập con M của tập hợp X sao cho tập con M có n^2 phần tử và không có ba phần tử nào lập thành một cấp số cộng.
Viết công thức tính số hoán vị của tập hợp gồm n phần tử n > 1 . Nêu ví dụ.
Tập hợp A gồm n phần tử
n
≥
4
. Biết rằng số tập hợp con chứa 4 phần tử của A bằng 20 lần số tập hợp con chứa 2 phần tử của A. Tìm số
k
∈
1
;
2
;
.
.
.
;
n
sao cho số tập hợp con chứa k phần tử của A là lớn nhất. A. 9...
Đọc tiếp
Tập hợp A gồm n phần tử n ≥ 4 . Biết rằng số tập hợp con chứa 4 phần tử của A bằng 20 lần số tập hợp con chứa 2 phần tử của A. Tìm số k ∈ 1 ; 2 ; . . . ; n sao cho số tập hợp con chứa k phần tử của A là lớn nhất.
A. 9
B. 8
C. 7
D. 6
Cho tập hợp X gồm 10 phần tử. Số các hoán vị của 10 phần tử của tập hợp X là
A. 10!.
B. 102.
C. 210.
D. 1010.
Cho tập hợp A gồm n phần tử
n
4
. Tìm n biết rằng trong số các phần tử của A có đúng 16n tập con có số phần tử là lẻ. A. n8 B. n9 C. n10 D. n16
Đọc tiếp
Cho tập hợp A gồm n phần tử n > 4 . Tìm n biết rằng trong số các phần tử của A có đúng 16n tập con có số phần tử là lẻ.
A. n=8
B. n=9
C. n=10
D. n=16
Cho tập hợp A có n phần tử
(
n
≥
4
)
. Biết rằng số tập con của A có 8 phần tử nhiều gấp 26 lần số tập con của A có 4 phần tử. Hãy tìm
k
∈
1
,
2
,
3...
Đọc tiếp
Cho tập hợp A có n phần tử ( n ≥ 4 ) . Biết rằng số tập con của A có 8 phần tử nhiều gấp 26 lần số tập con của A có 4 phần tử. Hãy tìm k ∈ 1 , 2 , 3 , . . . , n sao cho số tập con gồm k phần tử của A là nhiều nhất
A. k = 20
B. k = 11
C. k = 14
D. k = 10
Số các tổ hợp chập k của một tập hợp có n phần tử 1
≤
k
≤
n là :
A
.
C
n
k
n
!
(
n
-
k
)
!
B
.
C
n
k...
Đọc tiếp
Số các tổ hợp chập k của một tập hợp có n phần tử 1 ≤ k ≤ n là :
A . C n k = n ! ( n - k ) !
B . C n k = A n k k !
C . C n k = A n k ( n - k ) !
D . C n k = k ! ( n - k ) ! n !
Cho tập hợp A có 3 phần tử, số hoán vị các phần tử của A bằng
A. 5
B. 4
C. 6
D. 7
Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là
A
.
C
n
k
n
!
(
n
-
k
)
!
B
.
C
n
k
...
Đọc tiếp
Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là
A . C n k = n ! ( n - k ) !
B . C n k = n ! k ! ( n - k ) !
C . A n k = n ! ( n - k ) !
D . A n k = n ! k ! ( n - k ) !