Các câu hỏi tương tự
Cho tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ bên để được một cái hộp không nắp. Với giá trị nào của x thì hộp nhận được có thể tích lớn nhất? A. 6 B. 4 C. 3 D. 2
Đọc tiếp
Cho tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ bên để được một cái hộp không nắp. Với giá trị nào của x thì hộp nhận được có thể tích lớn nhất?
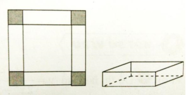
A. 6
B. 4
C. 3
D. 2
Một tấm kim loại hình chữ nhật có tổng chiều dài và chiều rộng là 18cm. Người ta cắt ở bốn gốc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng 3cm, rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Hỏi chiều rộng ban đầu của hình chữ nhật bằng bao nhiêu để hộp nhận được có thể tích lớn nhất ? A. 7,5 cm B. 9 cm C. 6 cm D. 3 cm
Đọc tiếp
Một tấm kim loại hình chữ nhật có tổng chiều dài và chiều rộng là 18cm. Người ta cắt ở bốn gốc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng 3cm, rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Hỏi chiều rộng ban đầu của hình chữ nhật bằng bao nhiêu để hộp nhận được có thể tích lớn nhất ?
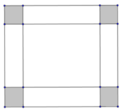
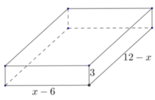
A. 7,5 cm
B. 9 cm
C. 6 cm
D. 3 cm
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất. A. x 4 B. x 2 C. x 1 D.
x
3
4
Đọc tiếp
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất.
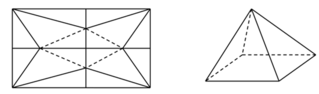
A. x = 4
B. x = 2
C. x = 1
D. x = 3 4
Người ta cắt bỏ 4 hình vuông nhỏ bằng nhau ở bốn góc của một tấm bìa hình vuông cạnh 60 cm và sử dụng phần còn lại để làm một cái hộp không nắp Tính cạnh hình vuông nhỏ để hộp có thể tích lớn nhất. Các bạn ơi giúp mình với
20 cm
5 cm
10 cm
15 cm
Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc một tấm bìa hình vuông cạnh 12cm rồi gấp lại thành hình hộp chữ nhật không có nắp. Nếu thể tích của cái hộp đó là thì cạnh của tấm bìa có độ dài là: A. 38cm B. 42cm C. 44cm D. 36cm
Đọc tiếp
Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc một tấm bìa hình vuông cạnh 12cm rồi gấp lại thành hình hộp chữ nhật không có nắp. Nếu thể tích của cái hộp đó là thì cạnh của tấm bìa có độ dài là:
A. 38cm
B. 42cm
C. 44cm
D. 36cm
từ 1 tấm tôn hình chữ nhật có kích thước 40cm và 60cm, người ta cắt bỏ bốn hình vuông ở bốn góc để lập dc 1 cái hộp ko nắp. để thể tích hộp lớn nhất thì cạnh của hình vuông cắt bỏ có giá trị gần đúng là
Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp. Khi dung tích của cái hộp đó là
4800
c
m
3
, tính độ dài cạnh của tấm bìa A. 42 cm B. 36 cm C. 44 cm D. 38 cm
Đọc tiếp
Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp. Khi dung tích của cái hộp đó là 4800 c m 3 , tính độ dài cạnh của tấm bìa
A. 42 cm
B. 36 cm
C. 44 cm
D. 38 cm
Một tấm kẽm hình vuông ABCD có cạnh bằng 30cm. Người ta gập tấm kẽm theo hai cạnh EF và GH cho đến khi AD và BC trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy. Giá trị của x để thể tích khối lăng trụ lớn nhất là:
Đọc tiếp
Một tấm kẽm hình vuông ABCD có cạnh bằng 30cm. Người ta gập tấm kẽm theo hai cạnh EF và GH cho đến khi AD và BC trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy. Giá trị của x để thể tích khối lăng trụ lớn nhất là:
![]()
![]()
![]()
![]()
Cho một tấm nhôm hình vuông có cạnh 6m. Người ta cắt ra một hình thang như hình vẽ. Tìm tổng x+y để diện tích hình thang EFGH đạt giá trị nhỏ nhất A. 7 B. 5 C.
7
2
2
D.
4
2
Đọc tiếp
Cho một tấm nhôm hình vuông có cạnh 6m. Người ta cắt ra một hình thang như hình vẽ. Tìm tổng x+y để diện tích hình thang EFGH đạt giá trị nhỏ nhất

A. 7
B. 5
C. 7 2 2
D. 4 2
Từ một miếng bìa hình vuông có cạnh bằng 5, người ta cắt 4 góc bìa 4 tứ giác bằng nhau và gập lại phần còn lại của tấm bìa để được một khối chóp tứ giác đều có cạnh đáy bằng x (xem hình vẽ bên). Cho chiều cao khối chóp tứ giác đều này bằng
5
2
. Tính giá trị của x A. x 1 B. x 2 C. x 3 D. x 4
Đọc tiếp
Từ một miếng bìa hình vuông có cạnh bằng 5, người ta cắt 4 góc bìa 4 tứ giác bằng nhau và gập lại phần còn lại của tấm bìa để được một khối chóp tứ giác đều có cạnh đáy bằng x (xem hình vẽ bên). Cho chiều cao khối chóp tứ giác đều này bằng 5 2 . Tính giá trị của x

A. x = 1
B. x = 2
C. x = 3
D. x = 4




