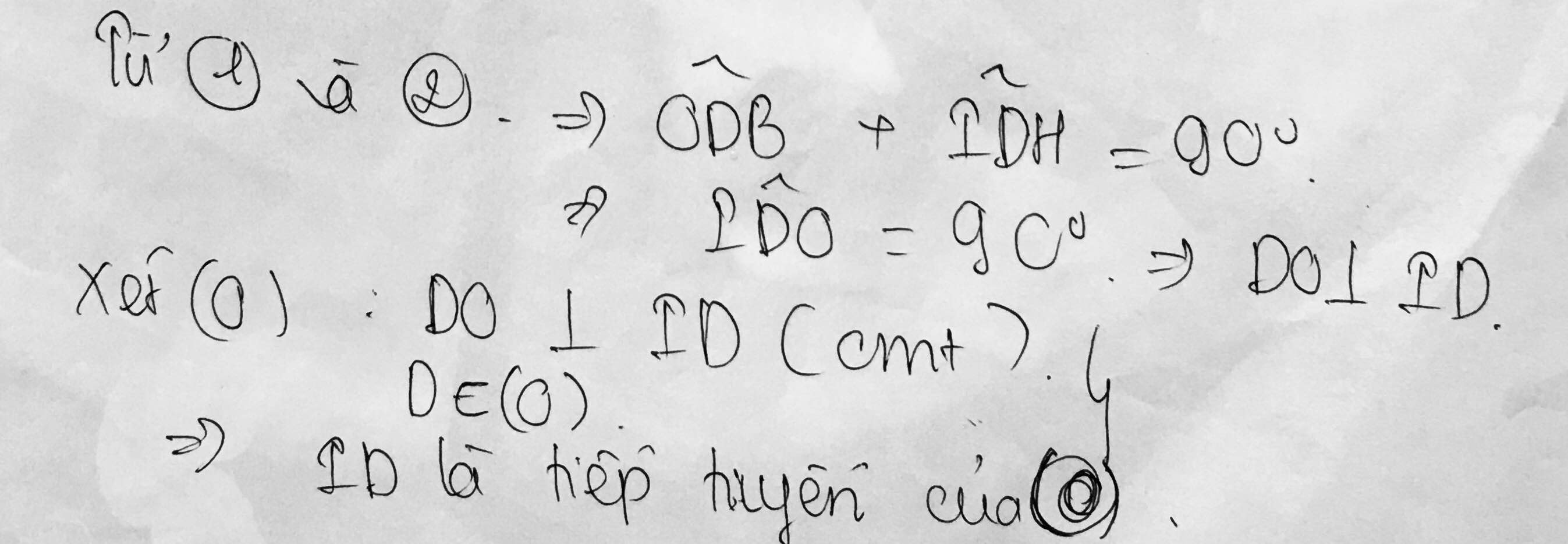Các câu hỏi tương tự
Cho tam giac ABC (ABAC) có ba góc nhọn. Vẽ đường tròn tâm (O) đường kính BC. Đường tròn này cắt AB tại E và cắt Ac ở D. BD cắt CE tại H.a. Chứng minh tứ giác ADHE là tứ giác nội tiếp.b. Chứng minh AD.AC AE.ABc. Chứng minh FH là tia phân giác của góc DFE, với F là giao điểm của AH và BC.d. Cho BC2a và góc BAC 60 độ. Chứng minh tứ giác DEFO là tứ giác nội tiếp và tính chu vi của đường tròn ngoại tiếp tứ giác này theo a.
Đọc tiếp
Cho tam giac ABC (AB<AC) có ba góc nhọn. Vẽ đường tròn tâm (O) đường kính BC. Đường tròn này cắt AB tại E và cắt Ac ở D. BD cắt CE tại H.
a. Chứng minh tứ giác ADHE là tứ giác nội tiếp.
b. Chứng minh AD.AC= AE.AB
c. Chứng minh FH là tia phân giác của góc DFE, với F là giao điểm của AH và BC.
d. Cho BC=2a và góc BAC= 60 độ. Chứng minh tứ giác DEFO là tứ giác nội tiếp và tính chu vi của đường tròn ngoại tiếp tứ giác này theo a.
Cho tam giác ABC có
B
A
C
^
45
0
, các góc B và C đều nhọn. Đường tròn đường kính BC cắt AB và AC lần lượt tai D và E. Gọi H là giao điểm của CD và BEa, Chứng minh AE BEb, Chứng minh tứ giác ADHE nội tiếp. Xác định tâm K của đường tròn ngoại tiếp tứ giác nàyc, Chứng minh OE là tiếp...
Đọc tiếp
Cho tam giác ABC có B A C ^ = 45 0 , các góc B và C đều nhọn. Đường tròn đường kính BC cắt AB và AC lần lượt tai D và E. Gọi H là giao điểm của CD và BE
a, Chứng minh AE = BE
b, Chứng minh tứ giác ADHE nội tiếp. Xác định tâm K của đường tròn ngoại tiếp tứ giác này
c, Chứng minh OE là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE
d, Cho BC = 2a. Tính diện tích viên phân cung D E ⏜ của đường tròn (O) theo a
Cho tam giác nhọn ABC với góc ABC60,BC,2a, ABAC. gọi (O) là đường tròn đường kính BC. đường tròn (O) cắt cạnh AB, AC tại điểm thứ hai là D và E. Đoạn BE và CD cắtt nhau tại Ha) chứng minh tứ giác ADHE nội tiếp (I) . Xác định tâm Ib) Tiếp tuyến tại C của đường tròn (O) cắt DI tại M. tính OB/OMc) Gọi F là giao. Điểm của AH và BC. Cho BF3a/4.Tính bán kính của đường tròn nội tiếp tam giác DEF theo a
Đọc tiếp
Cho tam giác nhọn ABC với góc ABC=60,BC,=2a, AB<AC. gọi (O) là đường tròn đường kính BC. đường tròn (O) cắt cạnh AB, AC tại điểm thứ hai là D và E. Đoạn BE và CD cắtt nhau tại H
a) chứng minh tứ giác ADHE nội tiếp (I) . Xác định tâm I
b) Tiếp tuyến tại C của đường tròn (O) cắt DI tại M. tính OB/OM
c) Gọi F là giao. Điểm của AH và BC. Cho BF=3a/4.Tính bán kính của đường tròn nội tiếp tam giác DEF theo a
B1: Cho tam giác ABC vuông tại A, biết AB 6cm, AC 8cm. Vẽ đường cao AH, đường tròn tâm O đường kính AH cắt AB tại E và cắt AC tại điểm F.a) Chứng minh tứ giác AEHF là hình chữ nhậtb) Chứng minh tứ giác BEFC nội tiếpc) Gọi I là trung điểm của BC.Chứng minh AI vuông góc với EFd) Gọi K là tâm của đường tròn ngoại tiếp tứ giác BEFC.Tính diện tích hình tròn tâm K.B2: Cho ABC nhọn, đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E và D, CE cắt BD tại Ha) Chứng minh tứ giác ADHE nội tiếpb) AH cắ...
Đọc tiếp
B1: Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 8cm. Vẽ đường cao AH, đường tròn tâm O đường kính AH cắt AB tại E và cắt AC tại điểm F.
a) Chứng minh tứ giác AEHF là hình chữ nhật
b) Chứng minh tứ giác BEFC nội tiếp
c) Gọi I là trung điểm của B
C.Chứng minh AI vuông góc với EF
d) Gọi K là tâm của đường tròn ngoại tiếp tứ giác BEF
C.Tính diện tích hình tròn tâm K.
B2: Cho ABC nhọn, đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E và D, CE cắt BD tại H
a) Chứng minh tứ giác ADHE nội tiếp
b) AH cắt BC tại F. chứng minh FA là tia phân giác của góc DFE
c) EF cắt đường tròn tại K ( K khác E). chứng minh DK// AF
d) Cho biết góc BCD = 450 , BC = 4 cm. Tính diện tích tam giác ABC
B 3: cho đường tròn ( O) và điểm A ở ngoài (O)sao cho OA = 3R. vẽ các tiếp tuyến AB, AC với đường tròn (O) ( B và C là hai tiếp tuyến )
a) Chứng minh tứ giác OBAC nội tiếp
b) Qua B kẻ đường thẳng song song với AC cắt ( O) tại D ( khác B). đường thẳng AD cắt ( O) tại E. chứng minh AB2= AE. AD
c) Chứng minh tia đối của tia EC là tia phân giác của góc BEA
d) Tính diện tích tam giác BDC theo R
B4: Cho tam giác ABC nhọn, AB >AC, nội tiếp (O,R), hai đường cao AH, CF cắt nhau tại H
a) Chứng minh tứ giác BDHF nội tiếp? Xác định tâm của đường tròn ngoại tiếp tứ giác đó
b) Tia BH cắt AC tại E. chứng minh HE.HB= HF.HC
c) Vẽ đường kính AK của (O). chứng minh AK vuông góc với EF
d) Trường hợp góc KBC= 450, BC = R. tính diện tích tam giác AHK theo R
B5: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Ba đương cao AE, BF, CK cắt nhau tại H. Tia AE, BF cắt đường tròn tâm O lần lượt tại I và J.
a) Chứng minh tứ giác AKHF nội tiếp đường tròn.
b) Chứng minh hai cung CI và CJ bằng nhau.
c) Chứng minh hai tam giác AFK và ABC đồng dạng với nhau
B6: Cho tam giác ABC nhọn nội tiếp đường tròn ( O; R ),các đường cao BE, CF .
a)Chứng minh tứ giác BFEC nội tiếp.
b)Chứng minh OA vuông góc với EF.
cho tam giác abc có 3 góc nhọn, dựng đường tròn tâm o đường kính bc cắt ab tại e và cắt ac tại f. gọi i là giao điểm của ce và bf chứng minh rằng oe là tiếp tuyến của đường tròn ngoại tiếp tứ giác aeif
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là t...
Đọc tiếp
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC
2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB
3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là trung điểm CH,BM cắt tiếp tuyến Ax của O tại P .chứng minh PC là tiếp tuyến của (O)
4.cho đường tròn O đường kính AB, M là một điểm trên OB.đường thẳng qua M vuông góc với AB tại M cắt O tại C và D. AC cắt BD tại P,AD cắt BC tại Q,AB cắt PQ tai I chứng minh IC,ID là tiếp tuyến của (O)
5.cho tam giác ABC nội tiếp đường tròn đường kính BC (AB<AC).T là một điểm thuộc OC.đường thẳng qua T vuông góc với BC cắt AC tại H và cắt tiếp tuyến tại A của O tại P.BH cắt (O) tại D. chứng minh PD là tiếp tuyến của O
6.cho tam giác ABC nội tiếp đường tròn O. phân giác góc BAC cắt BC tại D và cắt (O) tại M chứng minh BM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD
Cho tam giác ABC nhọn có ABAC. Vẽ đường tròn (O) đường kính BC cắt AB,AC lần lượt tại E,D. CE cắt BD tại H. AH cắt BC tại Ka. Chứng minh tứ giác BEHK nội tiếp và KA là phân giác góc EKDb. AI,AJ là các tiếp tuyến của (O) với tiếp điểm là I,J sao choD,J cùng nằm trên 1 nửa mặt phẳng bờ AK. Chứng minh góc IKE bằng góc DKJc. Chứng minh I,H,J thẳng hàngd. Kẻ đường thẳng qua K song song với ED cắt AB,CH lần lượt tại Q,S. Chứng minh K là trung điểm của QSAi giúp mình với :)))
Đọc tiếp
Cho tam giác ABC nhọn có AB<AC. Vẽ đường tròn (O) đường kính BC cắt
AB,AC lần lượt tại E,D. CE cắt BD tại H. AH cắt BC tại K
a. Chứng minh tứ giác BEHK nội tiếp và KA là phân giác góc EKD
b. AI,AJ là các tiếp tuyến của (O) với tiếp điểm là I,J sao choD,J cùng nằm trên 1 nửa
mặt phẳng bờ AK. Chứng minh góc IKE bằng góc DKJ
c. Chứng minh I,H,J thẳng hàng
d. Kẻ đường thẳng qua K song song với ED cắt AB,CH lần lượt tại Q,S. Chứng minh
K là trung điểm của QS
Ai giúp mình với :)))
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn ( O ). Ba đường cao AD,BE,CF cắt nhau tại H.a) Chứng minh tứ giác ABDE là tứ giác nội tiếp. Xác định tâm S của đường tròn ngoại tiếp tứ giác ABDE.b) Vẽ đường kính AK của ( O ). Chứng minh : AB×AC AD×AKc) Gọi I là trung điểm của HC. Chứng minh ST vuông góc ED.d) Đường phân giác trong của góc BAC cắt BC tại M và cắt đường tròn ( O ) tại N ( N khác A ). Gọi I là tâm đường tròn nội tiếp tam giác ACM.Gọi L là giao điểm của đường tròn ( O ) và CL. Ch...
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn ( O ). Ba đường cao AD,BE,CF cắt nhau tại H.
a) Chứng minh tứ giác ABDE là tứ giác nội tiếp. Xác định tâm S của đường tròn ngoại tiếp tứ giác ABDE.
b) Vẽ đường kính AK của ( O ). Chứng minh : AB×AC = AD×AK
c) Gọi I là trung điểm của HC. Chứng minh ST vuông góc ED.
d) Đường phân giác trong của góc BAC cắt BC tại M và cắt đường tròn ( O ) tại N ( N khác A ). Gọi I là tâm đường tròn nội tiếp tam giác ACM.
Gọi L là giao điểm của đường tròn ( O ) và CL. Chứng minh : N,O,L thẳng hàng.
e) Chứng minh ANKL là hình chữ nhật.
Cho tam giác ABC nhọn (AB AC) vẽ đường tròn tâm O có đường kính BC cắt hai cạnh AB và AC theo thứ tự tại E và F ,gọi H là giao điểm của BE và CF, AH cắt BC tại D. Gọi I là trung điểm AH a. Chứng minh tứ giác AEHF nội tiếp đường tròn tâm I và AD vuông góc BC b. Chứng minh tứ giác OEIF nội tiếp và 5 điểm O, D, E, I, F cùng thuộc một đường tròn C. cho biết BC 6 cm và góc A 60 độ Tính độ dài OI
Đọc tiếp
Cho tam giác ABC nhọn (AB < AC) vẽ đường tròn tâm O có đường kính BC cắt hai cạnh AB và AC theo thứ tự tại E và F ,gọi H là giao điểm của BE và CF, AH cắt BC tại D. Gọi I là trung điểm AH
a. Chứng minh tứ giác AEHF nội tiếp đường tròn tâm I và AD vuông góc BC
b. Chứng minh tứ giác OEIF nội tiếp và 5 điểm O, D, E, I, F cùng thuộc một đường tròn
C. cho biết BC = 6 cm và góc A = 60 độ Tính độ dài OI