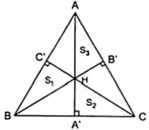
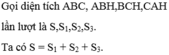
+ Các tam giác ABC và ABH có chung đáy AB nên tỉ số đường cao bằng tỉ số diện tích: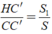
+ Tương tự: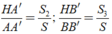
Khi đó ta có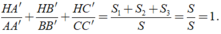

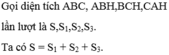
+ Các tam giác ABC và ABH có chung đáy AB nên tỉ số đường cao bằng tỉ số diện tích: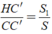
+ Tương tự: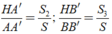
Khi đó ta có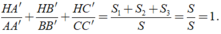
Cho tam giác ABC có góc B và góc C nhọn. Đường cao AA',BB',CC' cắt nhau tại H. Chứng minh
a) A'H.AA'=A'B.A'C
b) G là trọng tâm của tam giác ABC. Giả sử GH song song BC chứng minh A'A^2=3A'B.A'C
cho tam giác abc, trong đó b,c là góc nhọn. Các đường cao aa',bb',cc' cắt nhau tại h. gọi g là trọng tâm tam giác abc. Giả sử gh // bc. chứng minh: a'a2 = 3a'b.a'c
Cho tam giác ABC nhọn,các đường cao \(AA^,;BB^,;CC^,\)đồng quy tại H.Chứng minh rằng:\(\frac{AH}{A^,H}+\frac{BH}{B^,H}+\frac{CH}{C^,H}\ge6\)
cho tam giác ABC ba đường cao AA' ; BB' ; CC' gặp nhau tại H . Gọi H1;H2;H3 lần lượt là điểm đối xứng của H qua BC ; AC và AB.
a) tính tổng HA'/AA' + HB'/BB' + HC'/CC' và tổng AH1/AA' + BH2/BB'+ CH3/CC'
b) gọi I;E;F lần lượt là trung điểm của AH;BC;AC . Các đường trung trực của BC và AC cắt nhau tại O .Chứng minh : tứ giác AIEO là hình bình hành
c) các tia AO;BO;CO cắt BC;AC;AB tại A1;B1;C1. chứng minh rằng P= OA/OA1 + OB/OB1 + OC/OC1 >= 6
BAI NAY MINH LAM DUOC PHAN a .MONG CAC BAN GIUP MINH PHAN b ; c
Cho tam giác nhọn ABC. Ba đường thẳng AA1,BB1,CC1 cắt nhau ở H
chứng minh rằng A1H/A1A + B1H/B1B + C1H/C1C = 1
Cho tam giác nhọn ABC. Các đường cao AA',BB' , CC' cắt nhau ở H.
Chứng minh rằng:'\(\frac{HA'}{AA'}=\frac{HB'}{BB'}=\frac{HC'}{CC'}=1\)
Cho tam giác ABC có các đường cao AA', BB', CC' cắt nhau tại H. Chứng minh HA'/AA'=HB'/BB'=HC'/CC'
Cho tam giác ABC nhọn có các đường cao AA',BB',CC' và H là trực tâm
a,chứng minh BC'.BA+CB'.CA=BC^2
b,chứng minh rằng: HB.HC/AB.AC+HA.HB/BC.AC+HC.HA/BC.AB=1
c,Gọi D là trung điểm của BC.Qua H kẻ đường thẳng vuông góc với DH cắt AB,AC lần lượt tại M,N.Chứng minh:H là trung điểm của MN
Cho tam giác ABC nhọn có các đường cao AA',BB',CC' và H là trực tâm
a,chứng minh BC'.BA+CB'.CA=BC^2
b,chứng minh rằng: HB.HC/AB.AC+HA.HB/BC.AC+HC.HA/BC.AB=1
c,Gọi D là trung điểm của BC.Qua H kẻ đường thẳng vuông góc với DH cắt AB,AC lần lượt tại M,N.Chứng minh:H là trung điểm của MN