Xét tam giác MNP có QR // NP , áp đụng hệ quả định lí Ta- let ta có:
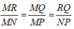
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

Chọn đáp án D
Xét tam giác MNP có QR // NP , áp đụng hệ quả định lí Ta- let ta có:
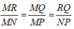
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

Chọn đáp án D
Cho tam giác MNP vuông tại M,MN=3cm,MP=4cm. I là trung điểm NP. Qua I kẻ đường thẳng vuông góc với NP cắt MP,MN lần lượt ở D và E.
a) tam giác MNP đồng dạng với tam giác IDP
b) Tính các cạnh của tam giác IDP
1) (C/m định lý về đg trung bình của hình thang)
Cho hình thang ABCD (AD//BC). M và P lần lượt là trung điểm của AB, CD. C/m MP song song với AD, BC & MP= (AD+BC):2
2) Cho tam giác MNP, D,E,F lần lượt là trung điểm của các cạnh NP, PM, MN. MD cắt EF tại O
a) Cm O là trung điểm của MD và EF
b) Cho chu vi tam giác DEF là 12cm, tính chu vi tam giác MNP
Chỉ cần chỉ ý cho mình thôi cũng đc
Bài 1. Cho tam giác ABC và tam giác MNP đồng dạng với nhau theo tỉ số 13 , 𝐴𝐵=3𝑐𝑚;𝑁𝑃=15. Tính các cạnh còn lại của hai tam giác biết chu vi tam giác ABC là 14cm.
Bài 2. Cho tam giác ABC có AB=3cm; AC=7cm và BC=5cm. Biết tam giác MPN đồng dạng với tam giác ABC có cạnh nhỏ nhất là 4,5 cm. Tính các cạnh còn lại của tam giác MPN.
Bài 3. Cho tam giác ABC có AB=5cm; BC=8cm; AC=7cm. Lấy điểm D nằm trên cạnh BC sao cho BD=2cm. Qua D kẻ đường thẳng song song với AB và AC lần lượt cắt AC và AB tại F và E.
a) Chứng minh BDE đồng dạng với DCF
b) Tính chu vi tứ giác AEDF.
Cho tam giác ABC , trên cạnh AB lấy điểm D sao cho DA/DB=1/2. Qua D kẻ đường thẳng song song với AC cắt BC tại I . Qua D kẻ đường thẳng song song với BC cắt AC tại E
A, tứ giác DECI là hình gì
B, tìm các cặp tam giác đồng dạng trên hình vẽ và tìm số đồng dạng
C, tính chu vi tam giác BDI và ADE , biết chu vi tam giác ABC là 12cm
CHO TAM GIAV1 MNP VUÔNG TẠI M CÓ \(\widehat{MNP}\)= \(60^0\). QUA M VÀ P VẼ HAI ĐƯỜNG THẲNG LẦN LƯỢT SONG SONG VỚI NP VÀ MN CHÚNG CẮT NHAU TAI Q. GỌI E LÀ TRUNG ĐIỂM CỦA NP, CHỨNG MINH TAM GIÁC EMQ LÀ TAM GIÁC VUÔNG
cho tam giác MNP vuông tại M có MN=4cm;MP=3cm
a)tính đọ dài NP và so sánh các góc của tam giác MNP
b)Trên tia đối tia PM lấy A sao cho P là trung điểm của đoạn thẳng AM.QUa P dựng đường thẳng vuông góc với AM cắt AN tại C.C/m tam giác CPM=tam giác CPA
c)C/m CM=CN
d)GỌi G là giao điểm của MC và NP.TÍnh NG
e)Từ A vẽ đường thẳng vuông góc với NP tại D.Vẽ tia Nx là tia phân giác của góc MNP,vẽ tia Ay là tian pg của PAD,tia Ay cắt các tia NP,Nx,NM lần lượt tại E,H,K.C/m tam giác NEK cân
Cho tam giác MNP.Gọi D,E,F lần lượt là trung điểm của các cạnh NP,PM,MN.Gọi O là giao điểm của MD và EF.
a)Chứng minh O là trung điểm của MD và EF
b)Cho chu vi tam giác DEF là 12cm.Tính chu vi tam giác MNP
c)Gọi I là trung điểm của MF,IE cắt đường thẳng NP tại K.Chứng minh PD=PK
Cho tam giác ABC có độ dài các cạnh A B = 4 c m , A C = 5 c m v à B C = 6 c m và tam giác MNP có độ dài các cạnh M N = 3 c m , M P = 2 c m , N P = 2 , 5 c m thì:
A. S A B C S M N P = 4
B. S M N P S A B C = 1 2
C. S M N P S A B C = 1 3
cho tam giác MNP vuông tại M . MN = 4cm, MP = 3cm. đường cao MI : a) Cm tam giác MNP và tam giác INM đồng dang => MN mũ 2 = NP . NI; b) tính độ dài NI và IP : c) gọi NE là tia phân giác của góc MNP . K là giao điểm NE và MI. cm EM/EP, NI/MN ; d) kẻ IH vuong góc với MN tại H. tính diện tích tam giác IMH