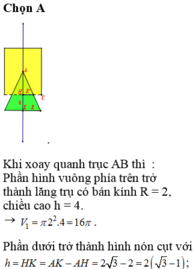
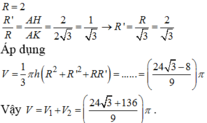Các câu hỏi tương tự
Cho hai hình vuông có cùng cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại (như hình vẽ). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY.
Đọc tiếp
Cho hai hình vuông có cùng cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại (như hình vẽ). 
Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY.
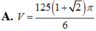
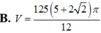
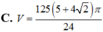
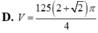
Cho tam giác vuông cân ABC có
A
B
A
C
a
2
và hình chữ nhật MNPQ với MQ2MN được xếp chồng lên nhau sao cho M, N lần lượt là trung điểm của AB, AC (như hình vẽ). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục AI, với I là trung điểm PQ.
Đọc tiếp
Cho tam giác vuông cân ABC có A B = A C = a 2 và hình chữ nhật MNPQ với MQ=2MN được xếp chồng lên nhau sao cho M, N lần lượt là trung điểm của AB, AC (như hình vẽ). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục AI, với I là trung điểm PQ.
![]()
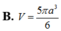
![]()
![]()
Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bằng hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía bên ngoài ta được hình 2. Khi quay hình 2 xung quanh trục d ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
Đọc tiếp
Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bằng hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía bên ngoài ta được hình 2. Khi quay hình 2 xung quanh trục d ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.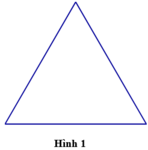

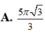
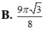
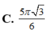
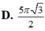
Cho tam giác ABC vuông ở A có AB2AC. M là một điểm thay đổi trên cạnh BC. Gọi H,K lần lượt là hình chiếu vuông góc của M trên AB,AC. Gọi V và V’ tương ứng là thể tích của vật thể tròn xoay tạo bởi tam giác ABC và hình chữ nhật MHAK khi quay quanh trục AB. Tỉ số
V
V
lớn nhất bằng
Đọc tiếp
Cho tam giác ABC vuông ở A có AB=2AC. M là một điểm thay đổi trên cạnh BC. Gọi H,K lần lượt là hình chiếu vuông góc của M trên AB,AC. Gọi V và V’ tương ứng là thể tích của vật thể tròn xoay tạo bởi tam giác ABC và hình chữ nhật MHAK khi quay quanh trục AB. Tỉ số V ' V lớn nhất bằng

![]()
![]()
![]()
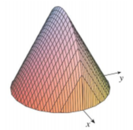
Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1 (hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x
-
1
≤
x
≤
1
thì được thiết diện là một tam giác đều. Tính thể tích V của vật thể đó A. V
3
B. V
3
3
C. V
4
3...
Đọc tiếp
Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1 (hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x - 1 ≤ x ≤ 1 thì được thiết diện là một tam giác đều. Tính thể tích V của vật thể đó
A. V = 3
B. V = 3 3
C. V = 4 3 3
D. V = π
Cho hình trụ tròn xoay, đáy là 2 đường tròn (C) tâm O và (C) tâm O’. Xét hình nón tròn xoay có đỉnh O’ và đáy là đường tròn (C). Xét hai mệnh đề sau: (I) Nếu thiết diện qua trục của hình nón là tam giác đều O’AB thì thiết diện qua trục của hình trụ là hình vuông ABB’A’. (II) Nếu thiết diện qua trục của hình trụ là hình vuông ABB’A’ thì thiết diện qua trục của hình nón là tam giác O’AB vuông cân tại O’. Hãy chọn câu đúng.
Đọc tiếp
Cho hình trụ tròn xoay, đáy là 2 đường tròn (C) tâm O và (C) tâm O’. Xét hình nón tròn xoay có đỉnh O’ và đáy là đường tròn (C). Xét hai mệnh đề sau: (I) Nếu thiết diện qua trục của hình nón là tam giác đều O’AB thì thiết diện qua trục của hình trụ là hình vuông ABB’A’. (II) Nếu thiết diện qua trục của hình trụ là hình vuông ABB’A’ thì thiết diện qua trục của hình nón là tam giác O’AB vuông cân tại O’. Hãy chọn câu đúng.
![]()
![]()
![]()
![]()
Cho hình lăng trụ ABC.ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của A lên đáy (ABC) trùng với trọng tâm của tam giác ABC và cạnh bên tạo với đáy một góc bằng 60
°
. Thể tích của hình lăng trụ là:A.
3
a
3
12
B.
3...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a, hình chiếu vuông góc của A' lên đáy (ABC) trùng với trọng tâm của tam giác ABC và cạnh bên tạo với đáy một góc bằng 60 ° . Thể tích của hình lăng trụ là:
A. 3 a 3 12 B. 3 a 3 8
C. 3 a 3 4 D. 3 a 3 2
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V1. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là V2. Tính tỉ số
V
1
V
2
.
Đọc tiếp
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V1. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là V2. Tính tỉ số V 1 V 2 .
![]()
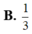
![]()
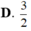
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox. A. . B. . C. . D. .
Đọc tiếp
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox.
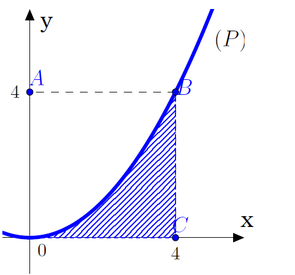
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.