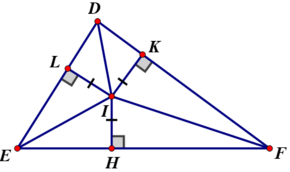
Gọi IH, IK, IL lần lượt là khoảng cách từ I đến EF, DF, DE.
Theo đề bài, điểm I cách đều ba cạnh của ΔDEF ⇒ IH = IK = IL
IL = IK ⇒ I cách đều hai cạnh của góc D ⇒ I nằm trên đường phân giác của góc D.
IH = IK ⇒ I cách đều hai cạnh của góc F ⇒ I nằm trên đường phân giác của góc F.
IH = IL ⇒ I cách đều hai cạnh của góc E ⇒ I nằm trên đường phân giác của góc E.
Từ 3 điều trên suy ra I là điểm chung của ba đường phân giác của tam giác DEF.










