Các câu hỏi tương tự
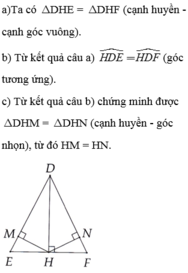
Cho tam giác DEF cân tại D. Gọi H là trung điểm của EF. a) C/m: t/giác DEH = t/giác DFH và DH vuông góc EF b) Kẻ HM vuông góc DE tại M, HN vuông góc DF tại N. C/m: t/giác HMN cân tại H c) C/m: MN// EF d) Qua E kẻ đường thẳng d vuông góc với DE, qua F kẻ đường thẳng d' vuông góc với DF, đường thẳng d cắt đường thẳng d' tại K. C/m: D, H , K thẳng hàng.
Cho tam giác ABC cân ở A. Trên cạnh BC lấy M, N sao cho BM = CN < BC/2. Kẻ ME vuông góc AB; NF vuông góc AC ( E thuộc AB; F thuộc AC ) EM cắt FN tại H. Chứng minh:
a) Tam giác ABM = tam giác CAN
b) Gọi D là trung điểm của MN. Chứng minh AD là tia phân giác của góc BAC
c) Tam giác MEB = tam giác NFC
d) EF // BC
e) A, D, H thẳng hàng
Cho tam giác ABC cân ở A. Trên cạnh BC lấy M, N sao cho BM = CN < BC/2. Kẻ ME vuông góc AB; NF vuông góc AC ( E thuộc AB; F thuộc AC ) EM cắt FN tại H. Chứng minh:
a) Tam giác ABM = tam giác CAN
b) Gọi D là trung điểm của MN. Chứng minh AD là tia phân giác của góc BAC
c) Tam giác MEB = tam giác NFC
d) EF // BC
e) A, D, H thẳng hàng
Cho tam giác ABC. Kẻ AH vuông góc BC ( H thuộc BC). Gọi D, E, F lần lượt là
các điểm nằm giữa A và H, nằm giữa B và H, nằm giữa C và H. Chứng minh rằng
chu vi tam giác DEF nhỏ hơn chu vi tam giác ABC. Với vị trí nào của các điểm D,
E, F thì chu vi tam giác DEF bằng ½ chu vi tam giác ABC.
Giúp với mik sắp phải nộp bài rồi
Cho tam giác ABC cân ở A. Trên cạnh BC lấy M, N sao cho BM = CN < BC/2. Kẻ ME vuông góc AB; NF vuông góc AC ( E thuộc AB; F thuộc AC ) EM cắt FN tại H. Chứng minh:
a) Tam giác ABM = tam giác CAN
b) Gọi D là trung điểm của MN. Chứng minh AD là tia phân giác của góc BAC
c) Tam giác MEB = tam giác NFC
d) EF // BC
e) A, D, H thẳng hàng
AI GIẢI NHANH VÀ ĐÚNG MIK SẼ TICK
Cho tam giác ABC cân ở A. Trên cạnh BC lấy M, N sao cho BM = CN < BC/2. Kẻ ME vuông góc AB; NF vuông góc AC ( E thuộc AB; F thuộc AC ) EM cắt FN tại H. Chứng minh:
a) Tam giác ABM = tam giác CAN
b) Gọi D là trung điểm của MN. Chứng minh AD là tia phân giác của góc BAC
c) Tam giác MEB = tam giác NFC
d) EF // BC
e) A, D, H thẳng hàng
AI GIẢI NHANH VÀ ĐÚNG MIK SẼ TICK
Cho tam giác ABC cân tại A. Tia phân giác góc BAC cắt cạnh BC tại M
a) Chứng minh ∆ A M B = ∆ A M C .
b) Kẻ M E ⊥ A B ( E ∈ A B ) , M F ⊥ A C ( F ∈ A C ) . Chứng minh tam giác AEF cân.
c) Chứng minh A M ⊥ E F .
d) Qua B kẻ đường thẳng song song với AC cắt đường thẳng FM tại I Chứng minh BE = BI
Giúp nhanh 5 phút với ạ!!!.
Bài 10. Cho tam giác DEF vuông tại D, có . Tia phân giác của góc F cắt DE tại I. Kẻ IH vuông góc với EF tại H ( ).
a. Chứng minh: DFI HFI
b. DFH là tam giác gì? Vì sao?.
c. Qua E kẻ đường thẳng vuông góc với DH tại N. Chứng minh EN // FI.
Bài 11. Cho cân ở A. Trên tia đối của các tia BC và CB lấy thứ tự hai điểm D và E sao cho BD CE.
a) Chứng minh cân
b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của .
c) Từ B và C kẻ BH, CK theo thứ tự vuông góc với AD và AE Chứng...
Đọc tiếp
Bài 10. Cho tam giác DEF vuông tại D, có . Tia phân giác của góc F cắt DE tại I. Kẻ IH vuông góc với EF tại H ( ). a. Chứng minh: DFI = HFI b. DFH là tam giác gì? Vì sao?. c. Qua E kẻ đường thẳng vuông góc với DH tại N. Chứng minh EN // FI. Bài 11. Cho cân ở A. Trên tia đối của các tia BC và CB lấy thứ tự hai điểm D và E sao cho BD = CE. a) Chứng minh cân b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của . c) Từ B và C kẻ BH, CK theo thứ tự vuông góc với AD và AE Chứng minh: BH = CK. d) Chứng minh ba đường thẳng AM, BH, CK đồng quy
Cho tam giác ABC có AB = AC . Gọi M là trung điểm của BC . Trên AB và AC lấy D và E sao cho AD = AE
a) Chứng minh : tam giác ABM = tam giác ACM
b) Chứng minh : AM vuông góc với BC
c) Chứng minh : tam giác ADM = tam giác AEM
d) Gọi H là trung điểm của EC . Trên tia đối của tia MH lấy F sao cho HM = HF . Chứng minh D , E , F thẳng hàng
Cho tam giác ABC có AB=AC, M là trung điểm của BC. Chứng minh rằng: tam giác AMB = tam giác AMC.
a) Trên cạnh AB lấy điểm D. Từ D kẻ đường vuông góc với AM tại K và kéo dài cắt cạnh AC TẠI E. Chứng minh AD=AE.
b) Trên tia đối của tia ED lấy điểm F sao cho EF=MC, gọi H là trung điểm của EC. Chứng minh rằng: ba điểm M, H, F thẳng hàng.