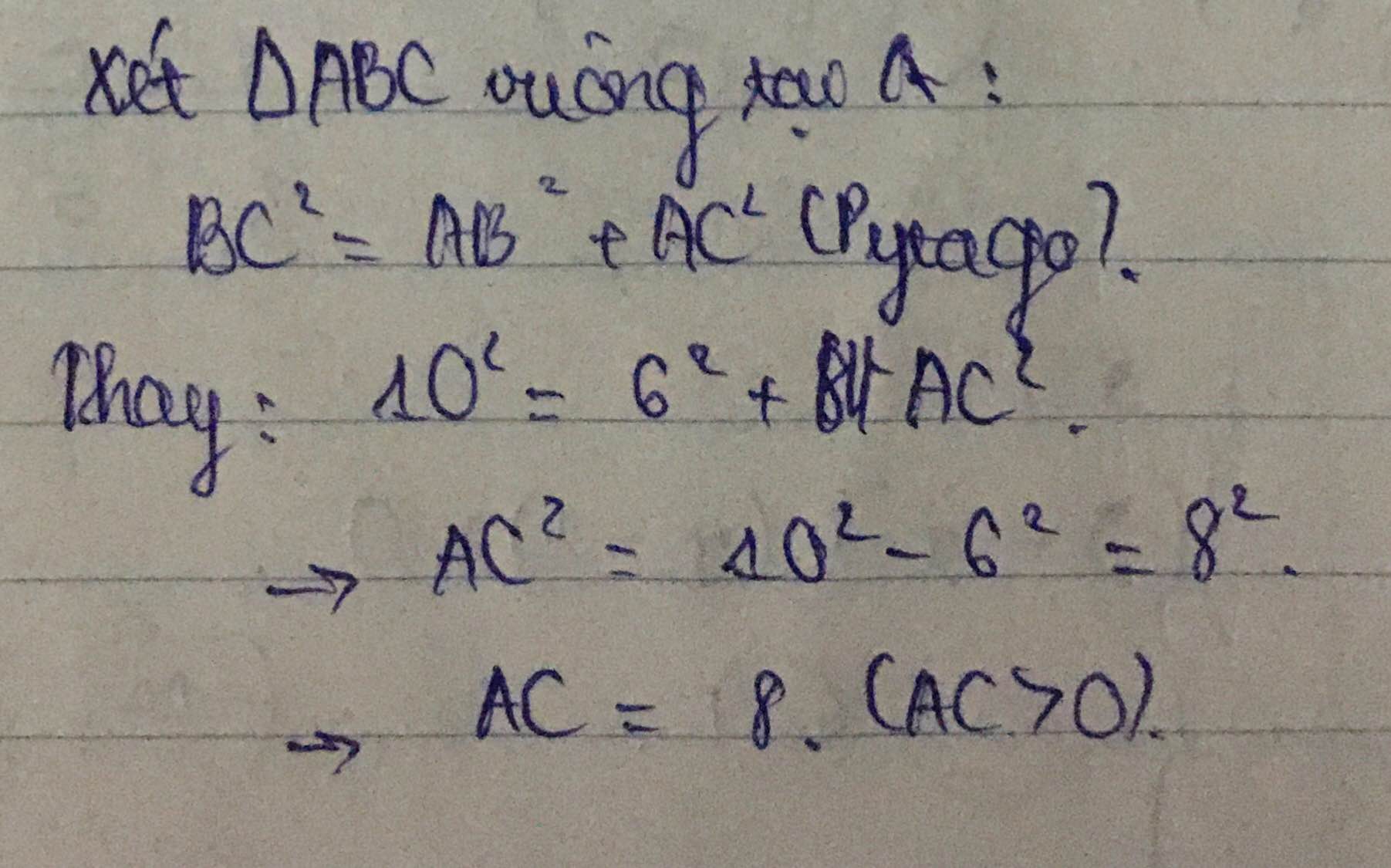Các câu hỏi tương tự
Câu 1: Cho tam giác ABC vuông tai A. Kẻ phân giác BD của widehat{ABC}( D thuộc AC), trên cạnh BC lấy E sao cho BA BE.a) Chứng minh tam giác ABD tam giác EBD và DE vuông góc với BC.b) Giả sử AD 6cm, DC 10cm. Tính độ dài đoạn EC.c) Biết tia ED cắt tia BA tại F và gọi M là trung điểm của đoạn FC. Chứng minh ba điểm B,D,M thẳng hàng.Câu 2: Cho tam giác ABC vuông tại A, có Ab 6cm ; BC 10cm.a) Tính ACb) Kẻ BD là phân giác của widehat{ABC} (D thuộc AC), kẻ DE vuông góc với BC ( E thuộc BC). Chứng...
Đọc tiếp
Câu 1: Cho tam giác ABC vuông tai A. Kẻ phân giác BD của \(\widehat{ABC}\)( D thuộc AC), trên cạnh BC lấy E sao cho BA = BE.
a) Chứng minh tam giác ABD = tam giác EBD và DE vuông góc với BC.
b) Giả sử AD= 6cm, DC = 10cm. Tính độ dài đoạn EC.
c) Biết tia ED cắt tia BA tại F và gọi M là trung điểm của đoạn FC. Chứng minh ba điểm B,D,M thẳng hàng.
Câu 2: Cho tam giác ABC vuông tại A, có Ab = 6cm ; BC = 10cm.
a) Tính AC
b) Kẻ BD là phân giác của \(\widehat{ABC}\) (D thuộc AC), kẻ DE vuông góc với BC ( E thuộc BC). Chứng minh DA = DE.
c) Chứng minh BD đi qua trung điểm của AE.
Câu 3: Cho góc xOy ( \(\widehat{xOy}\)không bằng 180o ) và tia Om là phân giác cuẩ góc xOy. Lấy điểm A thuộc Ox ; B thuộc Oy sao cho OA = OB. Gọi I là giao điểm của Om và AB.
a) Chứng minh tam giác AOI = tam giác BOI
b) Từ I kẻ IE thuộc Ox ( E thuộc Ox ) ; IF vuông góc với Oy ( F thuộc Oy ). Chứng minh tam giác EIF cân.
c) Lấy M trên Ox ( A nằm giữa O và M ) vẽ MN // Ab ( N thuộc Oy ), gọi H là trung điểm của MN =. Chứng minh 3 điểm O, I, H thẳng hàng.
LÀm ơn giúp với mai mình thi rồi. Vẽ cả hình nhé. Cảm ơn ~
1. Cho tam giác ABC vuông tại A. tia phân giác góc B cắt AC tại D. từ A kẻ AE vuông góc BD tại E và cắt BC tại MA. chứng minh tam giác ABC bằng tam giác MBEB. chứng minh DM vuông góc với BCC .Kẻ AH vuông góc với BC tại I. Chứng minh AM là tia phân giác của góc IACcâu 2: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ tia phân giác AD của góc A (D thuộc BC)A. chứng minh tam giác ABD bằng tam giác ACDB. Vẽ đường trung tuyến của tam giác ABC cắt cạnh AC tại G. chứng minh G là trọng tâm của tam...
Đọc tiếp
1. Cho tam giác ABC vuông tại A. tia phân giác góc B cắt AC tại D. từ A kẻ AE vuông góc BD tại E và cắt BC tại M
A. chứng minh tam giác ABC bằng tam giác MBE
B. chứng minh DM vuông góc với BC
C .Kẻ AH vuông góc với BC tại I. Chứng minh AM là tia phân giác của góc IAC
câu 2: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ tia phân giác AD của góc A (D thuộc BC)
A. chứng minh tam giác ABD bằng tam giác ACD
B. Vẽ đường trung tuyến của tam giác ABC cắt cạnh AC tại G. chứng minh G là trọng tâm của tam giác ABC
C. Gọi H là trung điểm của cạnh DC. qua h Vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh tam giác DEC cân
D. Chứng minh ba điểm B, G, E thẳng hàng
Câu 3 Cho tam giác ABC vuông tại A. Vẽ trung tuyến AM của tam giác ABC, Kẻ MH vuông góc với AC. Trên tia đối của tia MH đặt điểm K sao cho MK bằng MH
a. chứng minh tam giác MHC bằng tam giác MKB và BK vuông góc với KH
B. Chứng minh AB song song với HK và BK = AH.
C. Vẽ BH cắt AB tại g. Gọi I là trung điểm của AB. Chứng minh ba điểm C, G, I thẳng hàng
câu4 Cho tam giác ABC vuông tại A. gọi M là trung điểm cạnh BC. trên tia đối của tia MA lấy điểm D sao cho MD = MA.
A . chứng minh tam giác MCD bằng tam giác MBD và AC song song với BD
B. Gọi I là trung điểm AM, J là trung điểm BM. AJ cắt BI tại G. Chứng minh tam giác GAB là tam giác cân
Câu 5 cho tam giác ABC vuông tại A (AB bé hơn AC). vẽ BD là tia phân giác của góc ABC (D thuộc AC). trên đoạn BC lấy điểm E sao cho BE bằng BA
a chứng minh tam giác ABD bằng tam giác EBD .Từ đó suy ra góc BED là góc vuông
b. tia ED cắt tia BA tại EF. Chứng minh tam giác BED cân
C. Chứng minh tam giác AFC bằng tam giác ECF
D.Chứng minh: AB + AC >DE+BC
câu 6: Cho tam giác ABC vuông tại A. Vẽ đường phân phân giác BD của tam giác ABC và E là hình chiếu của D trên BC
a. chứng minh tam giác ABD bằng tam giác EBD và AE vuông góc với BD
B. Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh tam giác ABC bằng tam giác AFC
C. Qua A vẽ đường thẳng vuông góc với BC cắt CF tại G. Chứng minh ba điểm B, D, G thẳng hàng
câu 7: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ AD là phân giác của góc A (D thuộc BC)
A . Chứng minh tam giác ABD bằng tam giác ACD
B. lấy H là trung điểm của AB. Trên tia đối của tia HC lấy điểm K sao cho HK = HC. Chứng minh rằng AK = BC
c. CH cắt AD tại G. Chứng minh (BA+BC)÷6 >GH
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ MD vuông góc với BC( D thuộc BC)
a) Chứng minh BA = BD
b) Gọi E là giao điểm của hai đường thẳng d m và B Chứng minh tam giác ABC bằng tam giác DBE.
c) kẻ BH vuông góc MC(H thuộc MC) và AK vuông góc vs ME. Chứng minh MN là tia phân giác góc HMK.
d) Chứng minh ba điểm B, M, N thẳng hàng
cho tam giác ABC có AB =6cm, AC=8cm, BC=10cm
a) chứng ninh tam giác ABC vuông tại A
b) vẽ tia phân giác BD của góc ABC ( D thuộc AC) từ D vẽ DE vuông BC (E thuộc BC) .Chứng minh DA=DE
c) kéo dài ED và BA cắt nhau tại F. Chứng minh DF>DE
d)trên tia đối của tia AB lấy điểm M sao cho AM=CH. chứng minh ba điểm D,M,H thẳng hàng
Câu 4. Cho tam giác ABC, đường phân giác AD (D thuộc BC), kẻ tia Dx song song với AB, tia Dx cắt AC tại E. Chứng minh tam giác ADE là tam giác cân.Câu 5. Cho tam giác ABC có AB 6cm, AC 8cm và BC 10cm.a) Chứng tỏ tam giác ABC vuông.b) Kẻ phân giác BD và CE (D thuộc AC, E thuộc AB), BD và CE cắt nhau tại I. Tính góc BICCâu 6. Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC (H thuộc vẽ tia Bx song song với AH). Trên Bx lấy D sao cho BD AH.a) Chứng minh ΔAHB và ΔDHB bằng nhau.b) Nếu AC 12c...
Đọc tiếp
Câu 4. Cho tam giác ABC, đường phân giác AD (D thuộc BC), kẻ tia Dx song song với AB, tia Dx cắt AC tại E. Chứng minh tam giác ADE là tam giác cân.
Câu 5. Cho tam giác ABC có AB = 6cm, AC = 8cm và BC = 10cm.
a) Chứng tỏ tam giác ABC vuông.
b) Kẻ phân giác BD và CE (D thuộc AC, E thuộc AB), BD và CE cắt nhau tại I. Tính góc BIC
Câu 6. Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC (H thuộc vẽ tia Bx song song với AH). Trên Bx lấy D sao cho BD = AH.
a) Chứng minh ΔAHB và ΔDHB bằng nhau.
b) Nếu AC = 12cm; BC =15cm. Tính độ dài DH.
Câu 7. Cho tam giác ABC vuông tại B có góc B1=B2 ; Â=60o, kẻ BH vuông góc với AC (H thuộc AC). Qua B kẻ đường thẳng d song song với AC.
a) Tính góc ABH.
b) Chứng minh đường thẳng d vuông góc với BH.
Câu 8. Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M. Trên tia đối của tia CB lấy điểm N sao cho BM = CN.
a) Chứng minh ΔAMN là tam giác cân.
b) Kẻ BH vuông góc với AM (H thuộc AM), CK vuông góc với AN (K thuộc AN). Chứng minh rằng BH = CK.
c) Gọi O là giao điểm của BH và CK. Chứng minh ΔOBC cân.
d) Gọi D là trung điểm của BC. Chứng minh rằng A, D, O thẳng hàng.
Câu 9. Cho tam giác ABC, điểm D thuộc cạnh BC. Gọi M là trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME = MB. Trên tia đối của tia MC lấy F sao cho MF = MC. Chứng minh:
a) AE = BD;
b) AF // BC.
c) Ba điểm A, E, F thẳng hàng.
Câu 10. Cho tam giác ABC cân tại A, M là trung điểm của BC.
a) Chứng minh góc AFE = gócABC⇒EF//BC và ΔABM=ΔACM.
b) Chứng minh AM⊥BC.
c) Trên cạnh BA lấy điểm E. Trên cạnh CA lấy điểm F sao cho BE = CF. Chứng minh ΔEBC và ΔFCB bằng nhau.
d) Chứng minh EF // BC.
1. Cho ∆ABC vuông tại A (AB AC). Vẽ tia BD là phân giác của góc ABC (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BA BE.a. Chứng minh: ∆BAD ∆BEDb. Từ A kẻ AH ⊥ BC tại H. Chứng minh: AH // DEc. Trên tia đối của tia ED lấy điểm K sao cho ED EK. Chứng minh: Góc EKC góc ABC2.Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE BA. Phân giác góc B cắt AC tại D. a. Chứng minh ∆ABD Đồng ý∆EBD và DE ⊥ BCb. Gọi K là giao điểm của tia ED và tia BA. Chứng minh AK EC.c. Gọi M là trung điểm c...
Đọc tiếp
1. Cho ∆ABC vuông tại A (AB < AC). Vẽ tia BD là phân giác của góc ABC (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BA = BE.
a. Chứng minh: ∆BAD = ∆BED
b. Từ A kẻ AH ⊥ BC tại H. Chứng minh: AH // DE
c. Trên tia đối của tia ED lấy điểm K sao cho ED = EK. Chứng minh: Góc EKC = góc ABC
2.
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA. Phân giác góc B cắt AC tại D.
a. Chứng minh ∆ABD = Đồng ý∆EBD và DE ⊥ BC
b. Gọi K là giao điểm của tia ED và tia BA. Chứng minh AK = EC.
c. Gọi M là trung điểm của KC. Chứng minh ba điểm B, D, M thẳng hàng.
3.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm M sao cho BA = BM. Gọi E là trung điểm AM.
a.Chứng minh: ∆ABE = ∆MBE.
b. Gọi K là giao điểm BE và AC. Chứng minh: KM ⊥ BC,
c. Qua M vẽ đường thẳng song song với AC cắt BK tại F. Trên đoạn thẳng KC lấy điểm Q sao cho KQ = MF. Chứng minh: góc ABK = QMC
4
Cho tam giác ABC có AB = AC, lấy M là trung điểm của BC.
a) Chứng minh ∆ABM = ∆ACM
b) Kẻ ME ⊥ AB tại Em kẻ MF ⊥ AC tại F. Chứng minh AE = AF.
c) Gọi K là trung điểm của EF. Chứng minh ba điểm A, K, M thẳng hàng
d) Từ C kẻ đương thẳng song song với AM cắt tia BA tại D. Chứng minh A là trung điểm của BD.
Cho tam giác ABC vuông tại A, có góc B = 60 độ và AB = 5 cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC (E thuộc BC). Chứng minh:
a) Tam giác ABD = tam giác EBD
b) Tam giác ABE là tam giác đều
c) Tam giác AEC cân
d) Tính độ dài cạnh AC
e) Kéo dài DE cắt BA tại M. Gọi I là trung điểm của MC. Chứng minh ba điểm B, D, I thẳng hàng
Cho tam giác ABC vuông tại A có AC 6 cm, BC 10cm.
a) Tính độ dài cạnh AB và so sánh các góc của tam giác ABC.
b) Trên tia đối của tia AC lấy điểm D sao cho AD AC. Gọi K là trung điểm của cạnh BC, đường thẳng DK cắt cạnh AB tại M. Chứng minh BC BD và tính độ
dài đoạn thẳng AM.
c) Đường trung trực (d) của đoạn thẳng AB cắt đường thẳng DB tại Q. Chứng minh ba điểm C, M, Q thẳng hàng
Giúp mình bài này với
Mình cảm ơn trước nha
Đọc tiếp
Cho tam giác ABC vuông tại A có AC = 6 cm, BC = 10cm.
a) Tính độ dài cạnh AB và so sánh các góc của tam giác ABC.
b) Trên tia đối của tia AC lấy điểm D sao cho AD = AC. Gọi K là trung điểm của cạnh BC, đường thẳng DK cắt cạnh AB tại M. Chứng minh BC = BD và tính độ
dài đoạn thẳng AM.
c) Đường trung trực (d) của đoạn thẳng AB cắt đường thẳng DB tại Q. Chứng minh ba điểm C, M, Q thẳng hàng
Giúp mình bài này với
Mình cảm ơn trước nha
Co ta giác ABC vuông tại A, có góc C=30 độ, đường phân giác BD (B thuộc AC). Qua D kẻ đường thẳn vuông góc với BC tại M và cắt tia BA tại E.
a) Chứng minh AB=BM.
B) Chứng minh tam giác BCD cân và M là trung điểm BC.
C) Qua M kẻ đường thẳng vuông góc với Ac và cắt tia BD tại F. Chứng minh rẳng C,F,E thẳng hàng