a,i, Tìm được AB=3cm và AC = 6 3 cm
ii, Ta có: A B B D = A C B C = cos A B C ^ = cos 60 0 = cos A C D ^ = A C C D
b, Ta có: 1 A H 2 = 1 A C 2 + 1 A D 2

a,i, Tìm được AB=3cm và AC = 6 3 cm
ii, Ta có: A B B D = A C B C = cos A B C ^ = cos 60 0 = cos A C D ^ = A C C D
b, Ta có: 1 A H 2 = 1 A C 2 + 1 A D 2
BÀI 3. Cho tam giác ABC. Trên tia đối của tia BC lấy M sao cho BM = BA. Trên tia đối tia CB lấy N sao cho CN = CA. Qua M kẻ đường thẳng song song với AB, qua N kẻ đường thẳng song song với AC, chúng cắt nhau tại P.
a) Chứng minh MA là tia phân giác của PMB , NA là tia phân giác của PNC . b) Chứng minh PA là tia phân giác của MNP .
c) Gọi D là trung điểm AM, E là trung điểm AN, các đường thẳng BD, CE cắt nhau tại Q. Chứng minh QM = QN.
d) Chứng minh ba điểm P, A, Q thẳng hàng.
Bài 1.Cho tam giác ABC có trọng tâm G. Đường thẳng d đi qua G cắt hai cạnh AB và AC. CMR khoảng cách từ A đến d bằng tổng các khoảng cách từ B và C đến d.
Bài 2. Cho tam giác ABC cân tại A và đường cao AD. Từ D dựng DE vuông góc AB và DF vuông góc AC (E thuộc AB, F thuộc AC)
a) Chứng minh AD là trung trực của đoạn EF.
[B]b) [/B]Trên tia đối của tia DE lấy điểm G sao cho DG=DE. Chứng minh tam giác CEG vuông.
Bài 3. Cho tam giác ABC, vẽ tam giác vuông cân ABD cân tại B,A và D ở hai nửa mặt phẳng đối nhau bờ là đường thẳng BC. Vẽ tam giác vuông cân CBG cân tại B,G và A ở cùng nửa mặt phẳng bờ là đường thẳng BC. Chứng minh rằng GA vuông góc vớ DC.
Bài 4.Cho tam giác ABC trên tia đối của tia BA, CA lần lượt lấy điểm P,Q sao cho BP=CQ. Gọi M,N lần lượt là trung điểm của các đoạn BC,PQ. Đường thẳng MN cắt đường thẩngB,AC theo thứ tự tại B' và C'. Chứng minh rằng tam giác B'AC cân.
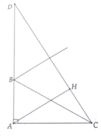
cho tam giác abc vuông tại a,\(\widehat{b}\)=60độ
a,tính ab,ac(lấy chữ số ở phần thập phân
b,kẻ ah vuông góc vs bc tại h.tính hb,hc
c,trên tia đối ba lấy d sao cho db=dc.chứng minh\(\frac{ab}{bd}=\frac{ac}{cd}\)
d,từ a kẻ đường thẳng song song vs phân giác\(\widehat{cbd}\)cắt cd tại k,chứng minh\(\frac{1}{kh.kc}=\frac{1}{ac^2}+\frac{1}{ad^2}\)
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia đối của tia AB lấy điểm K sao cho góc AKC = 600. D và E lần lượt là hình chiếu của H trên AB, AC. Qua A kẻ đường thẳng vuông góc với DE cắt BC tại M (M thuộc BC). Kẻ tia Cx là tia phân giác của góc ACB, qua M kẻ đường thẳng song song với AC cắt Cx tại F. Chứng minh BF vuông góc CF.
cho tam giác ABC vuông cân tại A cắt tai nội tiếp đường tròn tâm O. Tiếp tuyến tại B với đường tròn (O) CA tại D. Trên cạnh AB lấy điểm E ( E không trùng với A và B). Tia CE cắt đường tròn O tại F và cắt BD tại K. Tia BF cắt CD tại M.
a) chứng minh tam giác MAD đồng dạng với tam giác MFC
b) chứng minh tứ giác AFKD nội tiếp
c) Tia ME cắt BC tại H. Tứ giác MDBH là hình gì?
d) chứng minh AB.EB+CE.CF=BC^2
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D,E lần lượt là hình chiếu của H trên AB,AC. Biết AB=4cm, AC=6cm.
a) Chứng minh : AD.AB=AE.AC
b) Tính độ dài AE
c) Kẻ phân giác AI của góc BAC. Tính độ dài HI
d) Đường thẳng vuông góc với DE tại D cắt BC tại M. Chứng minh M là trung điểm của BH
Bài 2 : Cho tam giác ABC vuông ở A. Gỉa sử D là 1 điểm trên cạnh huyền BC và E.F lần lượt là hình chiếu của D lên các cạnh AB, AC. CMR : AE.EB + AF.FC=BD.DC
Cho (O; R) và một điểm A nằm ngoài (O) sao cho OA = 2R. Từ A vẽ tiếp tuyến AB của (O) (B là tiếp điểm)
a) Chứng minh tam giác ABO vuông tại B và tính độ dài AB theo R.
b) Từ B kẻ dây cung BC của (O) vuông góc với cạnh OA tại H. chứng minh AC là tiếp tuyến của (O)
c) Chứng minh tam giác ABC đều
d) Từ H kẻ đường thẳng vuông góc với AB tại D. Đường tròn đường kính AC cắt cạnh DC tại E. Gọi F là trung điểm của OB. Chứng minh ba điểm A, E, F thẳng hàng.
cho tam giác ABC vuông tại A, AB=27cm, AC=36cm
a. tính số đocác góc nhọn của tam giác ABC ( làm tròn đến độ )
b. vẽ đường thẳng vuông góc với đoạn BC tại B đường thẳng này cắt tia CA tại D . tính AD
c. vẽ E đối xứng với A qua BC . không tính AE . chứng minh 1/AE^2=1/4AB^2+1/4ac^2
d. trên nửa mặt phẳng bờ BCkhông chứa A lấy điểm M sao cho tam giác MBC vuông góc tại M . chứng minh AM là tia phân giác của góc BAC
cho tam giác ABC vuông tại A,đường cao AH,lấy D thuộc BC sao cho BD=BA.Kẻ DE vuông góc vs AC(E thuộc Ac
a) Chứng minh tam giác ADE=tam giác ADH?
b) Chứng minh AH+BC>AB+AC
c) Qua E kẻ đường thẳng song song với BC cắt HA tại I,cắt AB tại F,trên tia đói của tia HA lấy P sao cho HP=AI.Chứng minh góc BPF=gócCPE?