Đáp án D
Gọi M là trung điểm của BC.
Tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền BC nên:
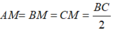
Suy ra, điểm M là tâm đường tròn ngoại tiếp tam giác ABC
Đáp án D
Gọi M là trung điểm của BC.
Tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền BC nên:
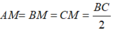
Suy ra, điểm M là tâm đường tròn ngoại tiếp tam giác ABC
Cho tam giác ABC nhọn có trực tâm H. Gọi M,N lần lượt là chân đường cao hạ từ B,C của tam giác ABC. Lấy D thuộc BC( D khác B,C), E là giao điểm của đường tròn ngoại tiếp tam giác CDM và đường tròn ngoại tiếp tam giác BDN(E khác B). CMR: A,E,D thẳng hàng
Cho tam giác ABC có các đường cao AD, BE, CF cắt nhau tại H. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. M là trung điểm của BC. a) Chứng minh 4 điểm B, F, E, C cùng thuộc một đường tròn. Xác định tâm của đường tròn đó. b) Chứng minh tam giác AEF và tam giác ABC đồng dạng. c) Chứng minh OM = 1/2 AH
cho tam giác ABC vuông tại A và AB<AC, đường cao AH . lấy điểm D saocho H là trung điểm của BD . gọi E là chân đường vuông góc hạ từ C đến đường thẳng AD a) chứng minh tứ giác AHEC nội tiếp ,xác định vị trí tâm O của đường tròn đó
b) chứng minh HA =HE
c) tìm thêm điều kiện ủa tam giác ABC để tứ giác AHEC là hình thang cân
Cho tam giác ngọn ABC hai đường cao hạ từ A và B cắt nhau tại H và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E chứng minh
a. CD=CE
b. CH vuông góc AB
c. Gọi I là giao điểm của AB và BC, K là giao điểm củaBE và AC. Chứng minh tứ giác AKIB nội tiếp xác định tâm đường tròn ngoại tiếp tứ giác AKIB
Giải giúp tớ với ạ mai mình phải nộp r help
Cho tam giác ABC không cân ở A,gọi M là trung điểm cạnh BC, D là hình chiếu vuông góc của A trên BC, E và F lần lượt là các hình chiếu vuông góc của B và C trên đường kính AA' của đường tròn ngoại tiếp tam giác ABC
CMR: M là tâm đường tròn ngoại tiếp tam giác DEF
Cho tam giác ABC (gócC#90 độ),các đường cao AD,BE cắt nhau tại H cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại I và K
a) CM: các tứ giác CDHE nội tiếp . Xác định tâm đường tròn ngoại tiếp tứ giác đó
b) CM: tam giác CKI cân
c)CM: AH=AK
d) Kẻ đường kính BOF (O là tâm đường tròn ngoại tiếp tam giác ABC). Gọi P là trung điểm của AC . CM: 3 điểm H,P,F thẳng hàng
Cho tam giác ABC vuông tại A I là trung điểm của BC . D là điểm nằm giữa I và C gọi E ,F theo thứ tự là tâm của đường tròn ngoại tiếp tam giác ABD và ACD. chứng minh E và F nằm trên đường tròn ngoại tiếp tam giác AID
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Trên cạnh BC lấy điểm D sao cho ^ABC = ^CAD. (K) là đường tròn nội tiếp tam giác ADC. E là chân đường phân giác xuất phát từ đỉnh B của tam giác ABC. Tia EK cắt đường tròn ngoại tiếp tam giác ABE tại L. CM tâm đường tròn ngoại tiếp tam giác BLC nằm trên (O) ?
Cho tam giác ABC có 3 góc nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC tại D, E. Gọi giao điểm của CD, BE là H. CM:
a) AH vuông góc BC
b) Trung trực của DH đi qua trung điểm I của đoạn thẳng AH
c) CM là tâm đường tròn ngoại tiếp tam giác ADE
d) OE là tiếp tuyến vòng tròn ngoại tiếp tam giác ADE
1) cho tam giác vuông ABC đường cao AH .gọi AD ;AE là phân giác các góc BAH và góc CAH .chứng minh rằng đường tròn nội tiếp tam giác BCA trùng với đường tròn ngoại tiếp tam giác ADE
2)cho tam giác ABC vuông tại A;gọi I là tâm đường tròn nội tiếp tam giác ABC ;các tiếp điểm trên BC;CA;AB lần lượt là D,E,F.gọi M là trung điểm của AC ,đường thẳng MI cắt các cạnh AB tại N ,đường thẳng DF cắt đường cao AH tại P .cmr tam giác APN cân