Các câu hỏi tương tự
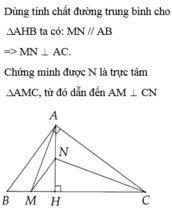
Cho \(\Delta\)ABC vuông tại A. Đường cao AH. Gọi M và N lần lượt là trung điểm của HB và HA. Chứng minh CN\(\perp\)AM
Cho tam giác ABC vuông gọc tại A . Kẻ đường cao AH . Gọi M và N lần lượt là trung điểm của các cạnh AB và AC . Chứng minh rằng MH vuông góc NH
Cho tam giác ABC vuông tại C . Kẻ đg cao CD. Gọi AM, CN lần lượt là trung tuyến của tam giác ADC và tg DBC. Chứng minh AM vuông góc CN
Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho Ha=Hd
a) chứng minh tam giac abh= tam giác DBH và tam giác AbD là tam giác cân
b) Gọi M,N lần lượt là trung điểm của Ac,Dc, G là giao điểm của dm và hc. Chứng minh 3 điểm A, g,n thẳng hàng
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC Kẻ MH vuông góc với AB tại H, MK vuông góc với AC tại K Chứng minh:
a) tam giác AMB = tam giác AMC b) AM vuông góc với BC c)HA = KA; HB = AC d) HK song song với BC
Giúp mình với, mik đng cần gấp. Cảm ơn các bạn nhìu!!!
Cho tam giác ABC, đường cao AH. D,E,F lần lượt là trung điểm của HB, HC, HA. Chứng minh rằng: CF vuông góc với AD, BF vuông góc với AE
Cho tam giác ABC vuông ở A có C=30 độ, đường cao AH. Trên đoạn HC lấy điểm M sao cho HB=HM. chứng minh:
a, AB=AM
b, Tam giác ABM là tam giác đều
c, Từ C kẻ CN vuông góc AM. chứng minh AH=CN
Cho tam giác ABC cân tại A , đường cao AH . Gọi E,F lần lượt là hình chiếu của H trên AC và AB . Gọi M là trung điểm của CB
a) Chứng minh : AM vuông góc với EF
b) Gọi N là trung điểm của AB và AH cắt NM tại D . Chứng minh : EF //DB
B1 :Cho tam giác ABC có 2 đường cao BD,CE. Gọi M,N là trung điểm của BC,DE. C/m MN vuông góc DE.
B2: Cho tam giác ABC cân tại A. H là trung điểm của BC. Kẻ HE vuông góc AC. Gọi I là trung điểm của HE. C/m AI vuông góc BE
B3: Cho tam giác ABC vuông tại A. M là trung điểm của BC. Đường cao AH. Kẻ HE vuông góc AC cắt AM tại N. C/m AM vuông góc BN