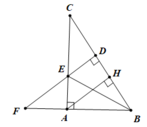
a. Hình vẽ (0.5 điểm)
Xét ΔABE và ΔDBE có:
Cạnh BE chung
BD = BA
⇒ ΔABE = ΔDBE (cạnh huyền – góc nhọn) (1 điểm)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC tại E, cắt BA tại F. Chứng minh
a. ΔABE = ΔBDE
b. BE là đường trung trực của AD
c. Tia BE là tia phân giác của tam giác ABC
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC tại E, cắt BA tại F. Chứng minh
c. Tia BE là tia phân giác của (ABC)
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC tại E, cắt BA tại F. Chứng minh
b. BE là đường trung trực của AD
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC tại điểm E.
d.Chứng minh: HD < DC
Cho tam giác ABC vuông tại A,đường cao AH. Trên tia BC lấy D sao cho BD =BA. Đường vuông góc với BC tại d cắt AC tại e. CM HD <DC
Cho ABC vuông tại A, đường cao AH. Trên cạnh BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC ở E.
Chứng minh tia AD là phân giác của góc HAC.
Cho tam giác ABC vuông tại A, đường cao AH. Trên cạnh BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC ở E. So sánh HD và DC.
cho tam giác ABC vuông tại A , tia phân giác góc B cắt AC tại E . Trên cạnh BC lấy điểm D sao cho BD=BA
a) chứng minh tam giác ABE = tam giác DBE
b) chứng minh ED vuông góc với BC
c) Tia BE cắt tia BA tại K . Chứng minh BK=BC
d) từ A kẻ AH vuông góc với BC(H €BC); AH giao BE tại I. Chứng minh AD là đường trung trực của IE
Cho tam giác ABC vuông tại A. Trên BC lấy điểm D sao ccho BD = BA. Tia phân giác của góc B cắt cạnh AC ở E. Qua C, vẽ đường thằng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. Chứng minh : Tam giác BAC = tam giác BDF và D, E, F thẳng hàng