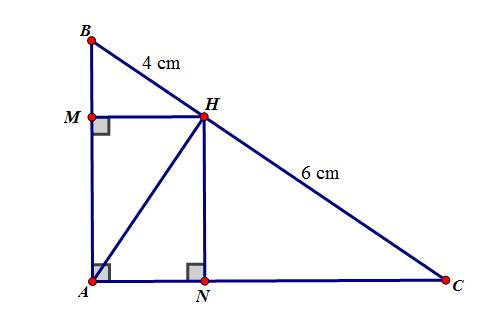
a, ΔABC vuông tại A \(\Rightarrow \angle BAC=90^o\)
M, N lần lượt là hình chiếu của H lên AB, AC \(\Rightarrow \angle HMA= \angle HNA =90^o \)
Tứ giác AMHN có: \(\angle BAC=\angle HMA=\angle HNA=90^o\)
Suy ra AMHN là hình chữ nhật.
b, Có: ΔAHB ∼ ΔCAB (g.g) \(\Rightarrow AB^2=BH.BC=4.(4+6)=40 \Rightarrow AB=2\sqrt{10}\)(cm)
Có: ΔAHC ∼ ΔBAC (g.g) \(\Rightarrow AC^2=CH.CB=6.(6+4)=60 \Rightarrow AC=2\sqrt{15}(cm)\)
SΔABC=\(\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.2.\sqrt{10}.2.\sqrt{15}=10\sqrt{6}\)(cm2)












