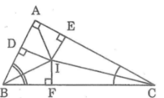
Tam giác vuông BAC có ∠A = 90o
Áp dụng định lí Pitago, ta có:
BC2 = AB2 + AC2
= 62 + 82 = 36 + 64 = 100
⇒ BC = 10 (cm)
Kẻ IF ⊥ BC
Xét hai tam giác vuông IDB và IFB, ta có:
∠(IDB) = ∠(IFB) = 90o
∠(DBI) = ∠(FBI) (gt)
cạnh huyền BI chung
Suy ra: ΔIDB = ΔIFB (cạnh huyền, góc nhọn)
Suy ra: DB = FB (hai cạnh tương ứng) (4)
Xét hai tam giác vuông IEC và IFC, ta có:
∠(IEC) = ∠(IFC) = 90o
∠(ECI) = ∠(FCI) (gt)
cạnh huyền CI chung
Suy ra: ΔIEC = ΔIFC (cạnh huyền, góc nhọn)
Suy ra: CE = CF (hai cạnh tương ứng) (5)
Mà: AD + AE = AB - DB + AC - CE
Suy ra: AD + AE = AB + AC - (DB + CE) (6)
Từ (4), (5) và (6) suy ra: AD + AE = AB + AC - (FB + FC)
= AB + AC - BC = 6 + 8 - 10 = 4 (cm)
Mà AD = AE (chứng minh trên)
Nên AD = AE = 4 : 2 = 2(cm).