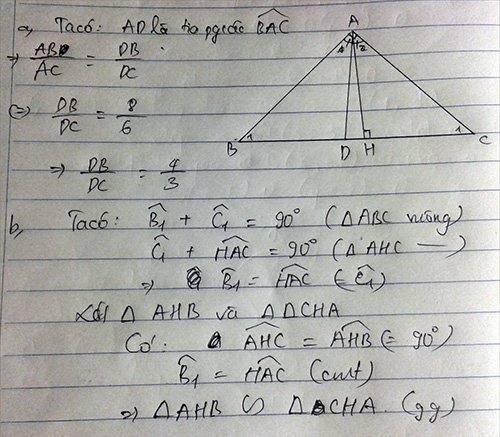Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A (D thuộc BC)
a, Tính DB, DC
b, Kẻ đường cao AH (H thuộc BC) . CMR: Tam giác AHB đồng dạng tam giác CHA.
c, Tính diện tích tam giác AHB và CHA.
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A (D thuộc BC) a/ Tính DB, DC. b/ Kẻ đường cao AH (H thuộc BC). C/m rằng tam giác AHB đồng dạng với tam giác CHA c/ tính S tam giác AHB, tam giác CHA
Cho tam giác ABC vuông tại A,Ab=8cm,AC=6cm,AD là tia phân giác góc A,D thuộc BC
a,Tính DB/Dc
b,Tính BC,từ đó tính DB,DC làm tròn kết quar 2 chữ số thập phân
c,Kẻ đường cao AH(H thuộc BC).Chứng minh rằng tam giác AHB đồng dạng với tam giác CHA.Tính Diện tích tam giác AHB/Diện tích tam giác CHA
d,Tính AH
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A (D thuộc BC)
a/ Tính DB, DC.
b/ Kẻ đường cao AH (H thuộc BC). C/m rằng tam giác AHB đồng dạng với tam giác CHA
c/ tính S tam giác AHB, tam giác CHA
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A (D thuộc BC). a) Tính DB/DC. b) Kẻ đường cao AH (H thuộc BC). Chứng minh tam giác AHB đồng dạng tam giác CHA
cho tam giác ABC vuông tại A, AB=8cm,AC=6cm. AD là tia phân giác của góc A(D thuộc BC), đường cao AH(H thuộc BC). Chứng minh rằng:
a, tính DB/DC
b, Tính BC từ đó tính DB,DC rồi làm tròn kết quả đến chữ số thập phân thứ 2
c, tam giác AHB đồng dạng với tam giác CHA. Tính S AHB/ S CHA
mCho tam giác abc vuông tại a có ab=8cm, ac=6cm, ad là tia p/gi của góc a(d thuộc bc)
a) tính \(\frac{db}{dc}\)
b) kẻ đường cao ah của tam giác abc(h thuộc bc). Chứng minh rằng tam giác ahb đồng dạng tam giác cha
c)tính tỉ số diện tích của hai tam giác ahb cà ahc
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A,
D BC .
a). Tính DB/DC
b). Kẻ đường cao AH ( H BC ). Chứng minh rằng: ΔAHB đồng dạng ΔCHA .
| c).Tính tỷ số diện tích của tam giác AHB và CHA |
d) Chứng minh AD2 =AB.AC – DB.DC
giúp mik với ạaa
cho tam giác ABC vuông tại A , AB=8cm ; AC=6cm ; AD là tia phân giác của góc A ; D thuộc BC
a, tính\(\frac{DB}{BC}\)
b, tính BC ; DB ; DC (làm tròn kết quả đến chữ số thập phân thứ 2 )
c, kẻ đường cao AH ; H thuộc BC. chứng minh tam giác AHB đồng dạng với tam giác CHA
d, tính tỉ số s\(\frac{AHB}{CHA}\)