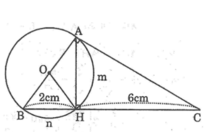
Trong tam giác vuông ABC có:
A H 2 = HB.HC =2.6=12
Suy ra: AH =2. 3 cm
Diện tích tam giác AHB:
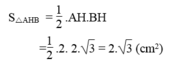
Tổng diện tích hai hình viên phân AmH và BnH bằng diện tích nửa hình tròn tâm O đường kính AB trừ diện tích tam giác AHB có:
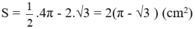

Trong tam giác vuông ABC có:
A H 2 = HB.HC =2.6=12
Suy ra: AH =2. 3 cm
Diện tích tam giác AHB:
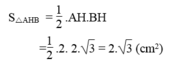
Tổng diện tích hai hình viên phân AmH và BnH bằng diện tích nửa hình tròn tâm O đường kính AB trừ diện tích tam giác AHB có:
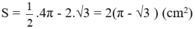
Cho tam giác ABC vuông ở A và đường cao AH.Vẽ đường tròn tam O đường kính AB.Biết BH = 2cm và HC = 6cm.Tính: Diện tích hình quạt tròn AOH (ứng với các cung nhỏ AH)
Cho tam giác ABC vuông ở A và đường cao AH.Vẽ đường tròn tam O đường kính AB.Biết BH = 2cm và HC = 6cm.Tính: Diện tích hình tròn (O)
Giải hộ mình với mai thi rồi
Cho tam giác ABC vuông tại A và đường cao AH vẽ đường tròn O đường kính AB, Biết BH = 2cm ; CH = 6cm. Tính :
a. Diện tích hình tròn
b. Diện tích hình quạt tròn AOH ( Ứng với cung tròn AH )
Bài 1: Cho tam giác MNQ vuông góc tại M và đường cao MH. Vẽ đường tròn tâm O đường kính MN biết NH=2cm; QH=6cm
a, Tính diện tích hình tròn tâm O
b, Diện tích hình quạt tròn MQH ứng với cung nhỏ MH
Cho mình thêm cái hình nhé. thankiu so much
Cho tam giác ABC vuông tại A có AB>AC, đường ca AH. Vẽ tròn đường kính BH cắt AB tại E, đường tròn đường kính HC cắt AC tại F.
a) Chứng minh tứ giác AEHF nội tiếp đường tròn ? Tìm tâm và đường kính của đường tròn ngoại tiếp tứ giác AEHF
b) Cứng minh AE.AB = AF.AC
c) Chứng minh bốn điểm B, E, F, C cùng nằm trên một đường tròn
d) Biết góc ABC bằng 30o, BH =4cm. tính tổng diện tích hình viên phân giới hạn bởi dây BE; dây HE và cung HE
Cho tam giác ABC vuông tại A , đường cao AH.Vẽ đường tròn tâm O đường kính AH. Đường tròn này cắt các cạnh AB, Ác theo thứ tự ở D và E.
a) CMR: D, O , E thẳng hàng .
B) các tiếp tuyến của đường tròn tâm Ở kẻ từ D và E cắt BC lần lượt tại M,N.CMR: M và N là trung điểm của HB và HC
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O (AB < AC). Hai đường cao AD, CE cắt nhau tại H
VẼ HÌNH VÀ GIẢI CHI TIẾT
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O (AB < AC). Hai đường cao AD, CE cắt nhau tại H
a) Giả sử góc A =60. Tính độ dài cung nhỏ BC và diện tích viên phân giới hạn bởi dây BC và cung nhỏ BC theo R
b) Kẻ đường kính AK cắt CE tại M, CK cắt AD tại F. Chứng minh: tứ giác BEHD nội tiếp và AH.AF=AM.AK
c) Gọi I là trung điểm của BC; EI cắt AK tại N. Chứng minh tứ giác EDNC là hình thang cân
cho tam gíc ABC nội tiếp đường tròn (O) bán kính R có góc C = 45 độ
a. tính diện tích hình quạt tròn AOB (ứng với cung nhỏ AB)
b. tính diện tích hình viên phân AmB (ứng với cung nhỏ AB)