+ Trong đường tròn đường kính MC:
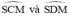 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 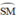
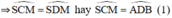
+ Trong đường tròn đường kính BC:
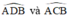 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 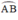
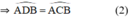


+ Trong đường tròn đường kính MC:
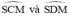 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 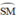
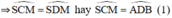
+ Trong đường tròn đường kính BC:
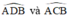 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 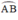
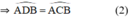

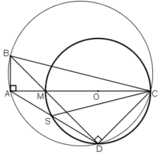
Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:
a) ABCD là một tứ giác nội tiếp
b) góc ABD bằng góc ACD
c) CA là tia phân giác của góc SCB
Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng: ABCD là một tứ giác nội tiếp
Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:
A B D ^ = A C D ^
Tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M, vẽ đường tròn đường kính MC cắt BC tại (D khác C) và cắt đường thẳng BM tại E ( E khác M). Đường thẳng AE cắt đường tròn tại S (S khác E). Chứng minh:
a) AM.MC=BM.ME
b) CA là tia phân giác góc SCB
c) Tam giác MDS cân
Bài 3. Cho tam giác ABC vuông ở A, với AC > AB. Trên AC lấy điểm M, vẽ đường tròn tâm O đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S. a) Chứng minh ABCD là tứ giác nội tiếp b) Chứng minh AC là tia phân giác của góc SCB c) Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy. d) Chứng minh DM là tia phân giác của góc ADE e) Chứng minh M là tâm đường tròn nội tiếp tam giác ADE
Cho △ ABC vuông tại A, với AC > AB. Trên AC lấy một điểm M, vẽ đường tròn (O) đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S
a. Chứng minh ABCD là tứ giác nội tiếp.
B. Chứng minh góc ABD = góc ABD
C. Chứng minh CA là tia phân giác của góc. AOB bằng 75°
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M. Vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng :
a) Tứ giác ABCD nội tiếp được đường tròn
b) Góc ACB = góc ACS
c) Tính diện tích và chu vi của đường tròn ngoại tiếp tứ giác ABCD, biết AB= 9cm, AC= 12 cm
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn tâm O có đường kính MC. Đường thẳng BM cắt đường tròn tâm O tại D. Đường thẳng AD AD cắt đường tròn tâm O tại S.
1) Chứng minh ABCD là tứ giác nội tiếp
2) Chứng minh CA là phân giác của góc SCB
3) Gọi E là giao điểm của BC với đường tròn tâm O. Chứng minh rằng các đường thẳng BA,EM,CD đồng quy.
4) Chứng minh DM là tia phân giác của góc ADE
5) Chứng minh điểm M là tâm đường tròn nội tiếp tam giác ADE
cho tam giác ABC vuông ở A, trên cạnh AC lấy điểm M vẽ đường tròn đường kính MC. Nối BM kéo dài cắt đường tròn tại D doạn thẳng AD cắt đường tròn ở K . CMR :
a) ABCD là tứ giác nội tiếp
b) CA là tia phân giác góc KCB