Chứng minh được ADME là hình bình hành Þ I là trung điểm của AM. Tương tự 2A. I thuộc đường trung bình của D ABC (đường thẳng đi qua trung điểm của AB và AC)
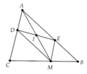
Cho tam giác ABC đều M là điểm bất kì trên cạnh BC Qua M kẻ đường thẳng song song với AC cắt AB tại D Qua M kẻ đường thẳng song song với AB cắt AC tại E Gọi I là trung điểm của am Chứng minh ba điểm D,I,E thẳng hàng b) khi M di chuyển trên BC thì I di chuyển trên đường nào
cho tam tam giác ABC .Gọi I là một điểm di chuyển trên BC. Qua I, kẻ đường thẳng song song với cạnh AC cắt cạnh AB tại M. Qua I, kẻ đường thẳng song song với cạnh AB cắt cacnhj AC tại N. Tìm vị trí của điểm I để MN song song với BC
Cho tam giác ABC. Gọi I là một điểm di chuyển trên cạnh BC. Qua I, kẻ đường thẳng song song với cạnh AC cắt cạnh AB tại M. Qua I, kẻ đường thẳng song song với cạnh AB cắt cạnh AC tại N.
1) Gọi O là trung điểm của AI. Chứng minh rằng ba điểm M, O, N thẳng hàng.
2) Kẻ MH, NK, AD vuông góc với BC lần lượt tại H, K, D. Chứng minh rằng MH + NK = AD.
3) Tìm vị trí của điểm I để MN song song với BC.
Cho tam giác ABC. Gọi I là một điểm di chuyển trên cạnh BC. Qua I, kẻ đường thẳng song song với cạnh AC cắt cạnh AB tại M. Qua I, kẻ đường thẳng song song với cạnh AB cắt cạnh AC tại N.
1) Gọi O là trung điểm của AI. Chứng minh rằng ba điểm M, O, N thẳng hàng.
2) Kẻ MH, NK, AD vuông góc với BC lần lượt tại H, K, D. Chứng minh rằng MH + NK = AD.
3) Tìm vị trí của điểm I để MN song song với BC.
Cho tam giác ABC. Gọi I là 1 điểm di chuyển trên cạnh BC. Qua I, kẻ đường thẳng song song với cạnh AC cắt cạnh AB tại M. Qua I, kẻ đường thẳng song song với cạnh AB cắt cạnh AC tại N.
1) Gọi O là trung điểm của AI. Chứng minh rằng 3 điểm M,O,N thẳng hàng
2) Kẻ MH,NK,AD vuông góc với BC lần lượt là H,K,D.C/m rằng MH+NK=AD
cho tam giác ABC có AB = AC . trên cạnh Bc lấy điểm M qua M kẻ đường thẳng song song với AC cắt cạnh AB tại N qua M kẻ đường thẳng song song cới AB, cắ t AC tại P
a . chứng minh AM, NP và đường thẳng đi qua trung điểm cạnh AB, cạnh AC đồng qui
b. tìm vị trí của M trên cạnh BC để AM vuông góc với NP
c. chứng minh rằng chu vi tứ giác APMN không thay đổi khi M di động trên cạnh BC
Cho tam giác ABC. Gọi I là một điểm di chuyển trên cạnh BC. Qua I, kẻ đường thẳng song song với cạnh AC tại M. Qua I, kẻ đường thẳng song song với AB cắt cạnh AC tại N.
1. Gọi O là trung điểm của AI. Chứng minh rằng ba điểm M, O, N thẳng hàng.
2. Kẻ MH, NK, AD vuông góc với BC lần lượt tại H, K, D. Chứng minh rằng MH+ NK= AD
3. Tìm vị trí của điểm I để MN song song với BC
Cho tam giác ABC, điểm M di động trên cạnh BC. Qua M kẻ các đường thẳng song song với cạnh AB và cạnh AC; chúng cắt cạnh AB và AC lần lượt tại các điểm D và E. Xác định điểm M sao cho diện tích của tứ giác ADME là lớn nhất.
Bài 30. Cho tam giác ABC. P là điểm tùy ý trên cạnh BC. Qua P kẻ đường thẳng song song với AB cắt AC tại E và kẻ đường thẳng song song với AC cắt AB tại E. Từ B kẻ đường thẳng song song với DE cắt PD tại N. Chứng minh rằng AN đi qua điểm cố định khi P thay đổi trên cạnh BC
