a) Vì BHCD có các cặp cạnh đối song song nên là hình bình hành.
b) Tứ giác ABCD có A B D ^ = A C D ^ = 90 0 m à B A C ^ = 60 0 nên B D C ^ = 120 0
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
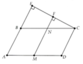
cho tam giác ABC trực tâm H, các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C và chúng cắt nhau tại D. Chứng minh rằng
a/ tứ giác BDCH là hình bình hành
b/ tính góc bcd biết góc bac = 60 độ
cho tam giác ABC và H là trực tậm các đường thẳng vuông góc với AB tại B,vuông góc với AC tại C cắt nhau ở D a)chứng minh tam giác BDCH là hình bình hành
b)tính góc BCD biết góc BAC=60 độ
Cho tam giác ABC, H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C và chúng cắt nhau tại D.
a) Chứng minh BDCH là hình bình hành.
b) Nếu tam giác ABC có góc A = 90 độ thì BDCH là hình gì?
c) Tìm điều kiện để tam giác BDCH là hình thoi.
cho tam giác ABC và H là trực tâm.các đường thẳng vuông góc với AB tại B,vuông góc với AC tại C cắt nhau ở D
a)chứng minh tứ giác BDCH là hình bình hành
b)tính số đo góc \(\widehat{BDC}\),biết \(\widehat{BAC}\)=600
15 tháng 1 2022 lúc 23:00
cho tam giác ABC, trực tâm H, các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau tại D. chứng minh:
a/ tứ giác BDCH là hinhg bình hành
b/ góc BAC+ góc BDC=1800
16 tháng 1 2022 lúc 12:17
cho tam giác ABC, trực tâm H, các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau tại D. chứng minh:
a/ tứ giác BDCH là hinhg bình hành
b/ góc BAC+ góc BDC=1800
Cho tam giác ABC, trực tâm H. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chứng minh rằng: a) BDCH là hình bình hành. b) ∠BAC + ∠BDC = 1800 c) H, M, D thẳng hàng ( M là trung điểm của BC) d) OM = 1/2AH ( O là trung điểm của AD). Giải và có hình với.
bài 3; cho tam giác ABC cân tại H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau tại D. CM; tứ giác BDCH là hình bình hành
cho tam giác ABC có 3 góc nhọn , H là truwjwjc tâm của tam giác ABC . Các đường thẳng vuông góc với AB tại B , vuông góc với AC tại C cắt nhau tại D .
a.CM: tứ gác BDCh là hình bình hành
b. Gọi I là trung điểm BC . đường vuông góc với BC tại I cắt AD tại M . Chứng minh : MI=1 phần 2