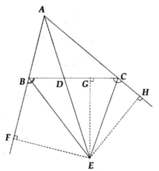
Gọi F,H,G lần lượt là hình chiếu vuông góc của điểm E xuống các đường thẳng AB, AC và BC.
Từ giả thiết suy ra EF = EG và EH = EG.
=> EF = EH nên E thuộc tia phân giác của góc BAC.
Mà AD là tia phân giác của góc BAC.
Vậy ba điểm A, D, E thẳng hàng.
Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng ba điểm B, I, K thẳng hàng.
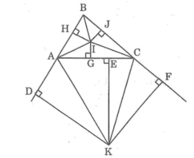
Cho tam giác ABC , góc A=120 độ. Các tia phân giác của góc A và C cắt nhau tại O, cắt các cạnh BC và AB lần lượt ở D và E. Đường phân giác góc ngoài tại đỉnh B của ΔABC cắt đường thẳng AC ở F. Chứng minh: a) BO⊥ BF b) góc BDF=góc ADF c) 3 điểm D,E,F thẳng hàng
cho △ ABC có A = 120 độ . Các đường phân giác AD và CE cắt nhau tại I , tia phân giác của góc ngoài tại đỉnh B cắt tại CA tại K
a) Chứng minh BE ⊥ BI
b) Chứng minh DK là phân giác của BDA
c) Chứng minh ba điểm D , E , K thẳng hàng
d) Tính DEC
cho △ ABC có A = 120 độ . Các đường phân giác AD và CE cắt nhau tại I , tia phân giác của góc ngoài tại đỉnh B cắt tại CA tại K
a) Chứng minh BE ⊥ BI
b) Chứng minh DK là phân giác của BDA
c) Chứng minh ba điểm D , E , K thẳng hàng
d) Tính DEC
Cho tam giác ABC , góc A=120 độ. Các tia phân giác của góc A và C cắt nhau tại O, cắt các cạnh BC và AB lần lượt ở D và E. Đường phân giác góc ngoài tại đỉnh B của ΔABC cắt đường thẳng AC ở F. Chứng minh:
a) BO⊥ BF
b) góc BDF=góc ADF
c) 3 điểm D,E,F thẳng hàng
Cho tam giác ABC , góc A=120 độ. Các tia phân giác của góc A và C cắt nhau tại O, cắt các cạnh BC và AB lần lượt ở D và E. Đường phân giác góc ngoài tại đỉnh B của ΔABC cắt đường thẳng AC ở F. Chứng minh:
a) BO⊥ BF
b) góc BDF=góc ADF
c) 3 điểm D,E,F thẳng hàng
cho tam giác ABC có ia phân giác trong của góc CAB và góc CBA cắt nhau tại D . Các tia phân giác ngoài ở đỉnh A và B cắt nhau ở E . Chứng minh CDE thảng hàng
Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng 3 điểm B, I, K thẳng hàng.
Cho tam giác ABC vuông cân tại đỉnh A, các tia phân giác trong AD và CE của góc A và góc C cắt nhau tại O . Đường phân giác ngoài góc B của tam giác ABC cắt AC tại F . Chứng minh :
a) Góc FBO = 90 độ
b) DF là tia phân giác của góc D của tam giác ABD
c) D,E,F thẳng hàng
