Chọn đáp án A
Tổng số đo 3 góc của 1 tam giác bằng 180° nên :
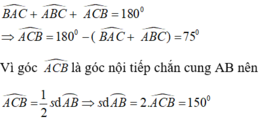
Chọn đáp án A
Tổng số đo 3 góc của 1 tam giác bằng 180° nên :
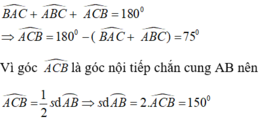
Tam giác đều ABC nội tiếp đường tròn tâm O bán kính R. Khi đó,góc BOC có số đo bằng bao nhiêu?
(A) 60 ° (B) 120 °
(C) 240 ° (D) Không tính được.
Trên đường tròn tâm O bán kính R lấy hai điểm A và B sao cho AB = R. Số đo góc
AOB chắn cung nhỏ AB có số đo là :
A.30 0 B. 60 0 C. 90 0 D . 120 0
Tam giác ABC nhọn có AB<AC, đường cao AD,BE,CF, trực tâm H nội tiếp (O) bán kính R
a) Chứng minh BFHD, BFEC nội tiếp
b) chứng minh góc DFE= 2 lần góc EBC
c) Cho số đo cung AB= 90 độ, số đo cung AC= 120 độ. Tính các góc của tam giác DÈ
d) Gọi I là trung điểm của CB. Chứng minh B,F,E,I thuộc 1 đường tròn
Cho tam giác ABC có góc A=600.Các điểm O,I lần lượt là tâm đường tròn ngoại tiếp,nội tiếp tam giác.Chứng minh rằng bốn điểm B,O,I,C cùng thuộc một đường tròn.
Cho tam giác ABC ( AB < AC ) nhọn nội tiếp đường tròn (O:R), với các đường cao AD, BE, CF và trực tâm H .
a) Chứng minh các tứ giác BFEC, BFHD nội tiếp .
b) Cho số đo cung BC = 90 độ , số đo cung AC = 120 độ . Tính số đo cung EFD
c) Tính độ dài đoạn thẳng BC theo R
cho tam giác ABC cân tại A,nội tiếp trong đường tròn tâm O đường cao AH,cắt đường tròn tại D.
a) chứng minh: AD là đường kính của đường tròn tâm O.
b) tính số đo góc ACD.
c) cho BC=24cm, AC=20cm. tính đường cao AH bằng bán kính đường tròn tâm O.
Bài 1. Cho tam giác ABC nội tiếp đường tròn (O), đường kính AB. Tính số đo các góc còn
lại của tam giác ABC nếu biết Ab = 40◦
Bài 3. Cho đường tròn (O;R), các điểm A,B thuộc (O) sao choAOB = 90◦
.
(a) Tính độ dài AB theo R.
(b) Gọi H là trung điểm AB. Chứng minh OH ⊥ AB.
Bài 4. Cho hình vuông ABCD có AB = a\(\sqrt{2}\)
(a) Chứng minh bốn điểm A,B,C,D cùng thuộc một đường tròn.
(b) Tính bán kính của đường tròn đi qua A,B,C,D theo a.
cho tam giác ABC có các góc đều nhọn, góc A=450 . Vẽ các đường cao BD và CE của tam giác ABC. Gọi H là giao điểm của BD và CE.
a) CM: tứ giác ADHE NỘI TIẾP
b/ CM HD=DC
C/ Tính tỉ số DE:BC
d/ Gọi O tâm đường tròn ngoại tiếp AB. CM : OA VUÔNG GÓC DE.
Cho tam giác ABC vuông tại A, kẻ đường cao AH và phân giác BE (H thuộc BC, E thuộc AC) Kẻ AD vuông góc BE ( D thuộc BE)
a) CM ADHB nội tiếp trong 1 đường tròn. Xác định tâm O của đường tròn đó
b) CM \(\widehat{EAD}\)= \(\widehat{HBD}\)và OD // HB
c) biết góc ABC=60 độ , và AB = a ( a>0) Tính theo a phần diện tích tam giác ABC nằm ngoài đường tròn O