Ta có, N là trung điểm của MC nên:
A N → = 1 2 A M → + A C → = 1 2 A M → + 1 2 A C → = 1 2 . 1 2 A B → + 1 2 A C → = 1 4 A B → + 1 2 A C →
Đáp án C
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Các điểm M(2; 3), N(0; -4), P(-1; 6) lần lượt là trung điểm các cạnh BC, CA, AB của tam giác ABC . Tọa độ đỉnh A của tam giác là:
A. (1; -10) B. (-3; 1) C. (-2; -7) D. (-3; -1)
Cho tam giác ABC với A(1; 4), B(3; -2), C(4; 5) và đường thẳng ∆: 2x – 5y + 3 = 0. Khẳng định nào sau đây là đúng?
A. Đường thẳng ∆ không cắt cạnh nào của tam giác
B. Đường thẳng ∆ cắt 1 cạnh của tam giác
C. Đường thẳng ∆ cắt 2 cạnh của tam giác
D. Đường thẳng ∆ cắt 3 cạnh của tam giác
Câu 8: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AD và BC, có bao nhiêu vectơ bằng với DM từ các điểm đã cho? A. 3. B. 4. C. 5. D. Câu 9: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chọn khẳng định đúng trong các khẳng định sau.A. AD BC . B. MQ PN . C. MN QP . D. AB DC .Câu 10: Cho tam giác ABC với trực tâm H, D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúngA. HA CD và AD CH .B....
Đọc tiếp
Câu 8: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AD và BC, có bao nhiêu vectơ bằng với DM từ các điểm đã cho? A. 3. B. 4. C. 5. D. Câu 9: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chọn khẳng định đúng trong các khẳng định sau.
A. AD BC . B. MQ PN . C. MN QP . D. AB DC .
Câu 10: Cho tam giác ABC với trực tâm H, D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúng
A. HA CD và AD CH .
B. HA CD và DA HC .
C. HA CD và AD HC .
D. HA CD và AD HC và OB OD .
Câu 1: Cho ABCD là hình vuông cạnh bằng 1. Khi đó độ dài của AC bằng
A. 1. B. 2. C. 2. D. 3.
Câu 2: Cho tam giác ABC vuông tại C có cạnh AC cm BC cm 4 , 3 . Độ dài của vectơ AB là
A. 7 . cm B. 6 . cm C. 5 . cm D. 4 . cm
Câu 3: Cho hình vuông ABCD tâm O, cạnh 2a. Độ dài vectơ DO bằng
A. 2 2. a B. 2 . 2 a C. a 2. D. 2 2. a
Câu 4: Cho đoạn thẳng AB cm 10 , điểm C thỏa mãn AC CB . Độ dài vectơ AC là
A. 10 . cm B. 5 . cm C. 20 . cm D. 15 . c
Cho tam giác ABC đều.Gọi D là điểm đối xứng của C qua AB.Vẽ đường tròn tâm D qua A, B và M là điểm bất kì trên đường tròn đó
M
≠
A
,
M
≠
B
Khẳng định nào sau đây đúng? A. Độ dài MA; MB; MC là độ dài ba cạnh của một tam giác vuông. B. MA, MB, MC là ba cạnh của 1 tam giác vuông. C. MA MB MC D. MC MB MA
Đọc tiếp
Cho tam giác ABC đều.Gọi D là điểm đối xứng của C qua AB.Vẽ đường tròn tâm D qua A, B và M là điểm bất kì trên đường tròn đó M ≠ A , M ≠ B Khẳng định nào sau đây đúng?
A. Độ dài MA; MB; MC là độ dài ba cạnh của một tam giác vuông.
B. MA, MB, MC là ba cạnh của 1 tam giác vuông.
C. MA= MB= MC
D. MC> MB> MA
Trong không gian Oxyz, cho ba điểm A(0; 0; 0), B(1; 2; 3), C(2; 3; 1). Gọi D là chân đường phân giác trong xuất phát từ đỉnh A của tam giác ABC. Trong các khẳng định dưới đây, khẳng định nào sai? A. AD ⊥ BC B. Một vectơ chỉ phương của đường thẳng AD là:
AB
→
+
AC
→
C. Một vectơ chỉ phương của đường thẳng AD là: D. Một vectơ chỉ phương của đường thẳng AD là: ...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(0; 0; 0), B(1; 2; 3), C(2; 3; 1). Gọi D là chân đường phân giác trong xuất phát từ đỉnh A của tam giác ABC. Trong các khẳng định dưới đây, khẳng định nào sai?
A. AD ⊥ BC
B. Một vectơ chỉ phương của đường thẳng AD là: AB → + AC →
C. Một vectơ chỉ phương của đường thẳng AD là: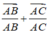 
D. Một vectơ chỉ phương của đường thẳng AD là: u AD → = (1; 1; -2)
Cho tam giác ABC có A(1; 3; 5), B(-4; 0; -2), C(3; 9; 6). Gọi G là trọng tâm tam giác ABC. Trong những khẳng định dưới đây, khẳng định nào sai? A. Tọa độ của điểm G là (0;4;3) B. AG ⊥ BC C. Phương trình tham số của đường thẳng OG là: x 0, y 4t, z 3t D. Đường thẳng OG nằm trong hai mặt phẳng: (P): x 0, (Q): 3y - 4z 0
Đọc tiếp
Cho tam giác ABC có A(1; 3; 5), B(-4; 0; -2), C(3; 9; 6). Gọi G là trọng tâm tam giác ABC. Trong những khẳng định dưới đây, khẳng định nào sai?
A. Tọa độ của điểm G là (0;4;3)
B. AG ⊥ BC
C. Phương trình tham số của đường thẳng OG là: x = 0, y = 4t, z = 3t
D. Đường thẳng OG nằm trong hai mặt phẳng: (P): x = 0, (Q): 3y - 4z = 0
Cho tam giác ABC có trọng tâm G và điểm M là trung điểm BC. khẳng định đúng là: A. Vt GA = 2 vt GM B. Vt GA = -2 vt GM C. Vt GM = 1/3 vt MA D. Vt AB + vt AC= vt AM Giải nhanh giúp em với ạ
Bài 4. Cho tam giác ABC có AM là đường trung tuyến và D là trung điểm của AM. a) Chứng minh rằng: 2 vec DA + vec DB + vec DC = vec 0 b) Chứng minh rằng: vec BD = 1 2 vec B vec A + 1 4 vec BC . c) Gọi E là điểm trên cạnh AC sao cho AE = 1/3 * A * C Chứng minh rằng B, D, E thẳng hàng. Tính tỉ số (DB)/(DE)
Cho tam giác ABC vuông cân tại A có
B
C
2
, M là trung điểm của BC. Khẳng định nào sau đây đúng A. B. C. D. Tất cả sai
Đọc tiếp
Cho tam giác ABC vuông cân tại A có B C = 2 , M là trung điểm của BC. Khẳng định nào sau đây đúng
A. 
B. 
C. 
D. Tất cả sai